Experimental Determination of the Free Energy of Formation of Freibergite Fahlore

Abstract - Values of = +21.504± 0.269 kJ× mol-1 at 573 K, and = +24.495± 0.393 kJ× mol-1 at 673 K, describe the molar free energy of formation of the hypothetical Cu-free endmember Ag₁₀Zn₂Sb₄S₁₃ from simple sulfides by the reaction

(1)

At each temperature, virtually identical Ag/(Ag+Cu) ratios in the coexisting solid solutions (Cu,Ag₁₀)Zn₂Sb₄S₁₃ (fahlore), (Ag, Cu)₃SbS₃(pyrargyrite), and (Ag,Cu)SbS₂ (miargyrite), with excess ZnS(sphalerite), were obtained by solid state reaction, in evacuated silica tubes, of several bulk compositions composed of a variety of combinations of sulfides and sulfosalts, for from 874 to 4503 hours. Results were confirmed by similar reactions at 473 K, and by synthesis reactions of finely ground mixtures of Ag₂S+Cu₂S+Sb₂S₃+ZnS, at 673 K for up to 9400 hours. The resulting silver-copper exchange data are used to derive values for the free energies of formation, from the simple sulfides, of the four (Cu,Ag)₁₀(Zn,Fe)₂Sb₄S₁₃ end-members, using established thermochemical data and the fahlore thermochemical model of Sack et al. (1987). Cell dimensions for high-Ag fahlores are presented, and the stability limits of As-free tetrahedrite-freibergite fahlores across the Fe-Zn join are predicted, and compared with experimental data.

The cubic (space group ) minerals: tennantite Cu₁₂As₄S₁₃, tetrahedrite Cu₁₂Sb₄S₁₃, and freibergite (Ag_5+xCu_7-x)Sb₄S₁₃ are part of the 'fahlore group', structurally approximated by:

(2)

(Cronstedt,1758; Ramdohr, 1969; Spiridonov, 1984) where Y = S, Se; X = As, Sb, Bi; M1+ = Ag, Cu ; M2+ = Fe, Zn, Cu , Hg, Cd, Sn, Mn, and possibly Pb, Ni, Co; and {} signify trigonal-planar, () tetrahedral, and [] octahedral sites. Fahlores have been used as qualitative indicators of zoning trends in hydrothermal ore deposits, where, unlike many sulfides and sulfosalts, they commonly retain their primary crystallization compositions (Barton and Skinner, 1979, p.384). Their potential power as petrogenetic indicator minerals has stimulated research into their mixing properties, however the free energies of formation of fahlore end-members have heretofore only been estimated by empirical algorithms using simple sulfide data (e.g. Craig and Barton, 1973). Here we present experimental equilibria at two temperatures, and derive free energies of formation from the sulfides for Ag-Cu-Fe-Zn-Sb fahlores.

Investigators of the system Ag₂S-Cu₂S-Sb₂S₃ include Gaudin and McGlashan (1938); Keighin and Honea (1969); Chen and Chang (1974), who note that fahlore is not a phase in the strict ternary (base of Fig. 1). Addition of relatively pure, refractory sphalerite ZnS (Fig. 1) stabilizes fahlore (Ag,Cu)₁₀Zn₂Sb₄S₁₃, and results are presented here for assemblages crystallized from bulk compositions within the dashed volume of Figure 1. Mixtures of the apices of Figure 1 (squares), and mixtures of complex phases (ovals: end-members of dashed tetrahedron), all result in sphalerite coexisting with virtually identical final compositions of fahlore, miargyrite, and pyrargyrite solid solutions. Thermodynamic analysis of the equilibrium compositions proceeds from published free energy data for pyrargyrite and miargyrite, and activity-composition relations for fahlore, pyrargyrite and miargyrite.

Experimental

Two types of synthesis experiment were used to approach equilibrium in fahlore-bearing assemblages. What we refer to as exchange experiments begin with Cu₁₀Zn₂Sb₄S₁₃ +Ag₃SbS₃+AgSbS₂+ZnS, with subsequent change in Ag/(Ag+Cu) ratios and relative abundances of the sulfosalts. Synthesis experiments begin with Ag₂S+Cu₂S+Sb₂S₃+ZnS, with subsequent nucleation and growth of sulfosalts. The bulk composition in each type of experiment corresponded to a fahlore solid solution of a specific Ag/(Ag+Cu), with excess ZnS added to most exchange experiments. A variety of Ag/(Ag+Cu) ratios and temperature conditions were investigated. Materials and evacuated silica tube methods (with vapor space minimized) closely follow Ebel and Sack (1989).

In exchange experiments, pure Cu₁₀Zn₂Sb₄S₁₃ ("CZS" fahlore, B41 of Ebel and Sack, 1989) was combined with pure AgSbS2, ZnS, and Ag3SbS3 or Ag2.85Cu0.45SbS3, in various ratios (Table 1) corresponding to bulk compositions in the interior of the four-phase tetrahedron (dashed, Fig. 1) defined by the coexistence of these end-member phases. Mixtures approximate fahlore stoichiometry, but with ZnS approximately doubled. In all cases, weighing errors favored the ZnS+Sb2S3 direction. Typically, about 200 mg of ground-together reactants were placed in a tube with approximately 0.1 mg of NH4Cl flux. The fahlore stability limit in this system cannot be approached from two directions (reversed), so only pyrargyrite compositions were reversed (e.g.-exps. T11 and T23). Equilibrium is very strongly suggested (cf.-Levin et al., 1969, p. 6) by the virtually identical results (Tables 3, 4) attained for (1) several bulk Ag/(Ag+Cu) ratios, (2) a variety of different initial phase assemblages, and (3) reaction durations differing by an order of magnitude. Control experiments (T20 and T8) with initial and final Ag/(Ag+Cu)=0.2 further support the conclusion that the experimental products represent equilibrium assemblages, consistent with our experience in sulfosalt synthesis and exchange. Fahlore was not seen after several thousand hour runs of control experiments with Cu-free fahlore bulk composition.

Synthesis experiments were attempts to manufacture (Cu,Ag)₁₀(Zn,Fe)₂Sb₄S₁₃ fahlores with Ag/(Cu+Ag)>0.45, following the techniques of Ebel and Sack (1989), and Ebel (1988). Synthetic Ag₂S, Cu₂S, Sb₂S₃, and ZnS or FeS were mixed in ~ 1 gram batches to make bulk compositions exactly equivalent to (Cu,Ag)₁₀(Zn,Fe)₂Sb₄S₁₃ (Table 2). Miniscule quantities of NH4Cl flux were added, and mixtures were reground at least once, in fresh alcohol. After tubes were quenched in water, random portions of the contents were removed and mounted for analysis. For Zn fahlores, small quantities of material removed after the first 30% of the total reaction time had compositions very similar to material analyzed much later. Reaction was more sluggish in the Fe synthesis experiment (NR3, Table 2). Nearly 100% yields were obtained for a great variety of mixed Fe-Zn Ag-bearing fahlores used as starting materials by Ebel and Sack (1989), using identical techniques but shorter heating durations.

Experimental products were mounted in Buhler epoxy, carbon coated, and analyzed on three of the four spectrometers of the CAMECA SX-50 electron microprobe at Purdue University. Two standard setups were used. For analysis of all phases, synthetic Ag₃SbS₃ for Ag (PET, La ); Cu₃SbS₃ for Cu (LiF, Ka ); CuSbS₂ for Sb (PET, La ) and S (PET, Ka ); Cu₁₀Zn₂Sb₄S₁₃ for Zn (LiF, Ka ); and Cu₁₀Fe₂Sb₄S₁₃ for Fe (LiF, Ka ) were used as standards (synthesis details in Ghosal and Sack, in prep; Ebel and Sack, 1989). This setup yields slightly low values for Sb in the 3-1-3 and 10-2-4-13 sulfosalts, and high S for fahlore, so a second setup was calibrated for S (PET, Ka ) using Cu₁₀Fe₂As₄S₁₃. The latter setup yielded slightly lower values for sulfur. Burn tests, recording counts for each of 300 seconds with a stationary 1, 5, 10, 20 or 30 micron diameter beam, showed steady count rates from the standards and similar mixed Ag-Cu phases. Nevertheless, a five or ten micron spot with ten second count time was used for all elements, and each analysis included a five second background count. Series of spot analyses were taken, spaced 8 to 20 microns apart on lines crossing one or more grain boundaries. Anomalous single analyses at grain boundaries were discarded. No significant compositional zoning was detected, except in 473 K experiments. Element weights percent reported here result from application of CAMECA's PAP correction scheme, and are believed to be accurate to better than ± 0.5 wt.% for all elements. Further details of experimental technique, analysis, burn tests, data, and photomicrographs of selected experiments, are reported elsewhere (Ebel, 1993).

Consistent with the bulk compositions, pyrargyrite (Ag,Cu)3SbS3 and (Cu,Ag)₁₀Zn₂Sb₄S₁₃-fahlore dominate the charge volumes. Pyrargyrite is most commonly mantled by fahlore, and sphalerite-pyrargyrite and sphalerite-myargyrite contacts are rare. Multi-phase grains are coarser than initial constituent powders. In contrast to the higer-temperature experiments, those at 473 K showed significant variability in fahlore composition, with the smallest fahlore grains gaining silver, but no Ag enrichment in the rims of large fahlore grains.

Craig and Scott (1976) review the literature on Zn and S deficiencies, and chromaticity in sphalerite: S-deficient sphalerite equilibrated above 1173 K shows green fluorescence, and brown color in sphalerite is due to excess sulfur. In the experiments reported here, product ZnS was light brown, and showed an intense blue fluorescence, similar to that of benitoite, under the electron beam. No significant silver or copper concentrations in the sphalerite were detected with the microprobe, and stoichiometry is 1:1 within probe error. Small amounts of macroscopically observable condensed sulfur in experiments T9, T11 and T14 indicate a high sulfur fugacity, but no phases off the Ag₂S-Cu₂S-Sb₂S₃ (± ZnS or FeS) plane were observed in any experiments.

Cell dimensions were calculated for products of several 673 K synthesis experiments, from d-spacings of the eight most prominent powder diffraction peaks (cf.-Ebel, 1993). For Zn-fahlore in W15, Ag/(Ag+Cu)=0.451, ao=10.637± 0.009. For Fe-fahlore NR3, Ag/(Ag+Cu)=0.729, ao=10.787± 0.004. After NR3 was annealed at 423 K for 891 hours, the measured cell edge was 10.628± 0.007 (cf.-Sack, 1987, Fig. 3).

Thermodynamics

The net transport reaction

(3)

describes the incorporation of silver by fahlore, and an analogous reaction describes incorporation of copper by the other sulfosalts. The concentration of the end-member Ag₁₀Zn₂Sb₄S₁₃ in fahlore is determined by the condition of equilibrium for (3):

(4)

in which represent the standard state molar Gibbs energies of formation of phases a from the simple sulfides Ag₂S, Cu₂S, Sb₂S₃, and ZnS, at temperature T(K), R being the gas constant, and represents the activity of endmember c in phase a . An expression for the activity of Ag₁₀Zn₂Sb₄S₁₃ in fahlore is provided by Sack et al., (1987, their Table II, parameters updated by Sack, 1992). Parameters (=9 kJ× mol-1, =14 kJ× mol-1 on a one site basis) for an assymetric regular solution model for pyrargyrite are provided by Harlov and Sack (1993). In Table 5 are summarized the values determined by Verduch and Wagner (1957; in part using data of Schenk et al. 1939), for the free energies of formation from the simple sulfides at 548 K and 673 K, of Ag3SbS3 (pyrargyrite) and AgSbS2 (miargyrite). Given the large Ag-Cu nonidealities seen in fahlore and pyrargyrite, and the very small solution of Cu, a symmetric regular solution with a nonideality of =15 kJ× mol-1 has been assumed to describe miargyrite. If ideal behavior (, the mole fraction of c in a ) is assumed for both pyrargyrite and miargyrite, calculated free energies of fahlores (Table 6) decrease by ~2.2%, and predicted Fe-fahlore Ag/(Ag+Cu) limits increase by ~4.2%. We treat sphalerite as a pure phase.

For the average result of the 673 K exchange experiments (Table 3), the derived value (equation 4) for the standard state free energy of formation from the sulfides of the Ag₁₀Zn₂Sb₄S₁₃ fahlore endmember is -23.960± 0.375 kJ× mol-1 (Table 6), the uncertainty reflecting only the standard deviation of calculated results. To extend this result to other antimony end-members requires consideration of the exchange reactions:

(5)

(6)

(7)

In equation (5), FeS is referred to the standard state in the sphalerite (sph) structure, and in (7) Ag is referred to the elemental (metal) standard state. Only reaction (7) is assumed to have non-negligible entropy (cf. Sack and Ghiorso, 1989). To obtain a value for the standard state free energy of formation of Ag₁₀Fe₂Sb₄S₁₃ by combining reactions (5) and (6), we refer FeS to the pyrrhotite (pot) standard state using the relation

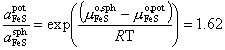(8)

derived by Fleet (1975), from the data of Barton and Toulmin (1966). Although the FeS-ZnS binary shows a very slight temperature dependence (Barton and Toulmin, 1966, Fig. 10), we have assumed that is temperature independent at the concentrations and temperatures of interest (cf.-Scott and Barnes, 1971, p. 656). Combining

(9)

with equation (5), we obtain at 673 K,

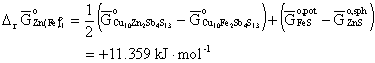. (10)

Then, at 673 K,

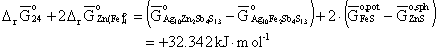(11)

and because we are interested in the standard states of formation from the sulfides, we have

. (12)

To extend these results to the copper-antimony endmembers, we apply standard state data for reactions (Table 5, eqns. 13-17) added to (7) according to

, (22)

obtaining a standard state Gibbs free energy for the reaction

(23)

.

Then we have

, (24)

and

. (25)

Discussion

One can predict the maximum Ag/(Cu+Ag) in fahlore in Fe-bearing systems from the results for Zn-fahlores. To do this, we use experimental results for the Zn system to calculate energies for the reactions

(26)

and

, (27)

and add each to equation (6), above. Referring FeS to the pyrrhotite standard state (Craig and Scott, 1976, p. CS-24) , the compositions of all three sulfosalts may then be calculated, employing the Fe-analog of condition (4), above. Results of such calculation appear in Table 6 and in Figure 2. These results are consistent with experiment NR3, which provides only a lower bound on the differential stabilities of Fe versus Zn Ag-fahlores at 673 K, due to the absence of miargyrite and the low initial Ag/(Ag+Cu) (Table 2).

We can also test the derived 673 K formation energies by extrapolating them to 573 K and 473 K. In the absence of heat capacity data, one may suppose for reaction (3). One may also suppose that the entropy of this reaction is due solely to the random disordering of Ag and Zn on tetrahedral sites in fahlore (see (2), above). For this assumption, the entropy change of reaction (3) is

. (28)

Our results at 573 K are in close agreement with the conclusion that this "zero-point entropy addition" accounts for the temperature dependence of fahlore composition in the assemblage pyrargyrite+miargyrite+fahlore+sphalerite. The results at 473 K, although only representing very local equilibrium, and interpreted outside the temperature range of some of the thermochemical data (e.g.-equation 8, above), are also consistent with this conclusion.

Acknowledgements: R.O. Sack acknowledges material support from the National Science Foundation (grant EAR-92-19083). D.S. Ebel thanks Purdue University for its commitment to basic research. Technical assistance was provided by Carl Hager, Earl Geist, William Azeredo, Subhabrata Ghosal, and Janet Lovell. Critical reviews by Paul B. Barton, Jr., Robert R. Seal, II, and W.H. MacLean were most helpful.

BARTON M.D. (1980) The Ag-Au-S system. Econ. Geol. 75, 303-316.

BARTON P.B., JR., and SKINNER B.J. (1979) Sulfide mineral stabilities. In Geochemistry of Hydrothermal Ore Deposits, 2nd edn. (ed. H.L. BARNES), Chap. 7, pp 278-403. J. Wiley & Sons.

BARTON P.B., JR., and TOULMIN P., III, (1966) Phase relations involving sphalerite in the Fe-Zn-S system. Econ. Geol. 61, 815-849.

CHEN, T.T., and CHANG L.L.Y. (1974) Investigations in the systems Ag₂S-Cu₂S-Bi₂S₃ and Ag₂S-Cu₂S-Sb₂S₃. Canadian Mineralogist 12, 404-410.

CRAIG J.R. and BARTON P.B., JR. (1973) Thermochemical approximations for sulfosalts. Econ. Geol. 68, 493-506.

CRAIG J.R., and SCOTT S. D. (1976) Sulfide phase equilibria. In Sulfide Mineralogy, ch. 5. (ed. P. H. RIBBE). Mineralogical Society of America.

CRONSTEDT A. (1758) Mineralogie; eller Mineral-Rickets Upstallning. Magellan, London.

EBEL D.S. (1988) Argentian zinc-iron tetrahedrite-tennantite thermochemistry. M.S. thesis, Purdue University.

EBEL D.S. (1993) Thermodynamics of Mineral Solutions. Ph.D. thesis, Purdue University.

EBEL D.S., and SACK R.O., (1989) Ag-Cu and As-Sb exchange energies in tetrahedrite-tennantite fahlores. Geochim. Cosmochim. Acta 53, 2301-2309.

EBEL D.S., and SACK R. O., (1991) Arsenic-silver incompatibility in fahlore. Mineral. Mag. 55, 521-528.

FLEET M.E. (1975) Thermodynamic properties of (Zn,Fe)S solid solutions at 850° C. Amer. Mineral. 60, 466-470.

HARLOV D.E. and SACK R.O. (1993) Thermodynamic properties of polybasitem, pyrargyrite, and skinnerite solutions in the system Ag₂S-Cu₂S-Sb₂S₃. Geological Society of America Abstracts with Program.

GAUDIN A.M. and McGLASHAN D.W. (1938) Sulphide silver minerals - A contribution to their pyrosynthesis and to their identification by selective iridescent filming. Econ. Geol. 33, 143-193.

KEIGHIN W., and HONEA M. (1969) The system Ag-Sb-S from 600oC to 200oC. Mineral. Depos. 4, 153-171.

KUBASCHEWSKI O., EVANS E.L., and ALCOCK C.B. (1967) Metallurgical Thermochemistry, 4th Ed. Pergamon Press.

Levin E.E., Robins C.R., and McMurdie H.F. (1969) Phase Diagrams for Ceramists, 2nd. Ed. The American Ceramic Society, Columbus, Ohio.

O'LEARY M.J., and SACK R. O., (1987) Fe-Zn exchange reaction between tetrahedrite and sphalerite in natural environments. Contrib. Mineral. Petrol. 96, 415-425.

POTTER R.W., II (1977) An electrochemical investigation of the system copper-sulfur. Econ. Geol. 72, 1524-1542.

RAMDOHR P. (1969) The Ore Minerals and Their Intergrowths, pp. 554-562. Pergamon Press.

RICHARDSON F.D., and JEFFES J.H.E. (1952) The thermodynamics of substances of interest in iron and steel making. III. Sulfides. Jour. Iron Steel Inst. 171, 165-175.

ROBIE R.A., WIGGINS L. B., BARTON P.B., Jr., and HEMINGWAY B.S., (1985) Low temperature heat capacity and entropy of chalcopyrite (CuFeS₂): Estimates of the standard molar enthalpy and Gibbs free energy of formation of chalcopyrite and bornite (Cu₅FeS₄). J. Chem. Therm. 17, 481-488.

SACK R.O. (1992) Thermochemistry of tetrahedrite-tennantite fahlores. In The Stability of Minerals (ed. N.L. ROSS and G.D. PRICE), pp. 243-266. Chapman and Hall, London.

SACK R.O., EBEL D.S., and O'LEARY M.J. (1987) Tennahedrite (sic) thermochemistry and metal zoning. In Chemical Transort in Metasomatic Processes (ed. H.C. Helgeson), pp. 701-731. D. Reidel, Dordrecht, Holland.

SACK R.O., and GHIORSO M.S. (1989) Importance of considerations of mixing properties in establishing an internally consistent thermodynamic database: Thermochemistry of minerals in the system Mg₂SiO₄-Fe₂SiO₄-SiO₂. Contrib. Mineral. Petrol. 102, 41-68.

SCHENCK R., HOFFMAN I., KNEPPER W., and VOGLER H. (1939) Gleichgewichtestudien über erzbildende Sulfide, I. Zeitschr. anorg. allg. Chemie 240, 173-195.

SCOTT S.D. and BARNES H.L. (1971) Sphalerite geothermometry and geobarometry. Econ. Geol. 66, 653-669.

SPIRIDONOV E.M. (1984) Species and varieties of fahlore (tetrahedrite-tennantite) minerals and their rational nomenclature. Dokl. Akad. Nauk. SSR 279, 166-172.

TOULMIN P., III, and BARTON P.B., Jr. (1964) A thermodynamic study of pyrite and pyrrhotite. Geochim. Cosmochim. Acta. 28, 641-671.

VERDUCH A.G., and WAGNER C. (1957) Contributions to the thermodynamics of the systems PbS-Sb₂S₃, Cu₂S-Sb₂S₃, Ag₂S-Sb₂S₃ and Ag-Sb. J. Phys. Chem. 61, 558-562.

TABLE 3. Summary of results of exchange experiments. Duration (e.g.-874 hours) at specified temperature is noted below experiment label. Data are mean element weights percent of n microprobe analyses of pyrargyrite, miargyrite, fahlore and sphalerite, with (parenthetically) 1000x 1s standard deviation. Ag/(Ag+Cu) are atomic ratios in the phases.

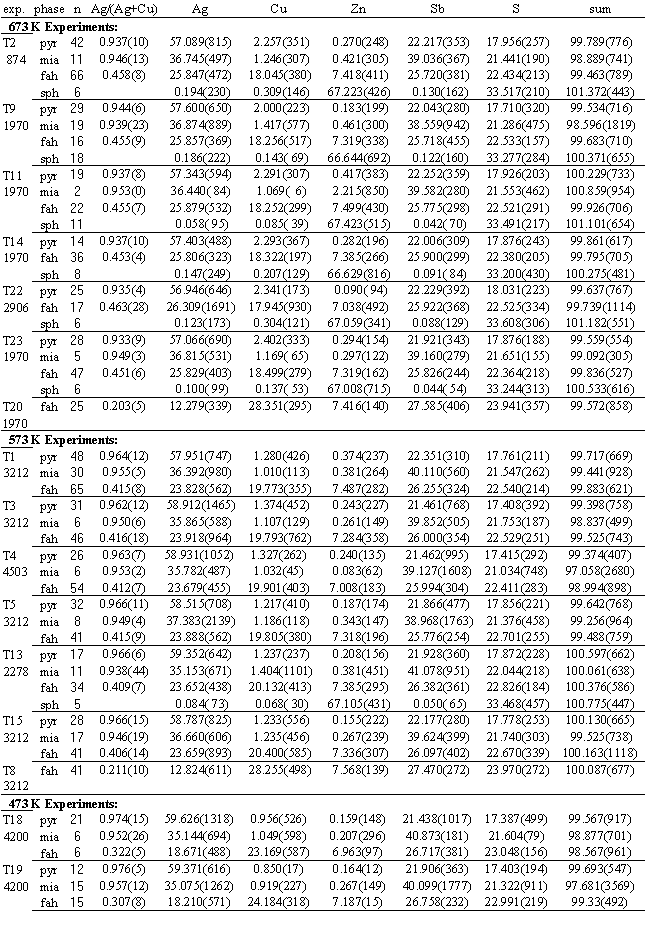
TABLE 4. Summary of results of fahlore synthesis experiments. Data are mean element weights percent for n microprobe analyses of pyrargyrite, fahlore and sphalerite or pyrrhotite, with (parenthetically) 1000x 1s standard deviation. Ag/(Ag+Cu) are mean atomic ratios.

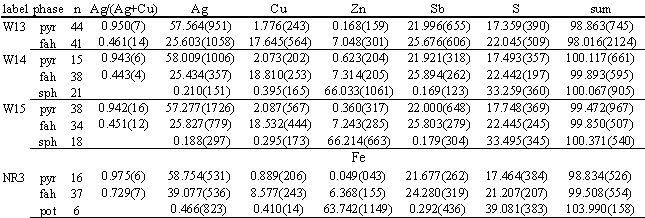
TABLE 5. Expressions for standard state free energy changes (J× mol-1) of sulfide reactions, temperature (T) in degrees K. Equations are referred to in text by numbers in column one. Data with * are taken from Barton and Skinner (1979, Table 7-2), who assign all the data presented here an uncertainty of less than 4184 J. The standard state for sulfur is the diatomic gas at one atmosphere.

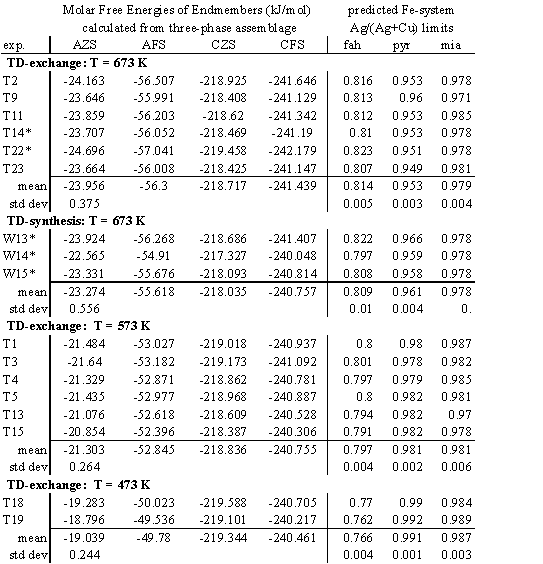
* Miargyrite could not be analyzed in these experiments (see Table 3), so the

value Ag/(Ag+Cu) = 0.946 in miargyrite was assumed in these calculations.

(Figure 1, Ebel and Sack, 1993)

Back to:
The University of Chicago

Department of the Geophysical Sciences at the University of Chicago

home page.

Last modified May 31, 1998.