D.S. Ebel
Department of the Geophysical Sciences, The University of Chicago, 5734 S. Ellis Ave,
Chicago, Illinois, U.S.A. 60637
and
A.J. Naldrett
Department of Geology, University of Toronto, Earth Sciences Centre, Toronto, Ontario,Canada M5S 3B1
Abstract
Tie line compositions of (Fe, Ni, Cu)1-xS (monosulfide solid solution, mss) and Fe-Ni-Cu-S liquid, in the presence of sulfur vapor, have been quenched from temperatures between 900°
C and 1180°
C. More than 80 bulk compositions on both sulfur-rich and sulfur-poor sides of the mss field were investigated by sealed silica tube techniques.
Qualitative observations of wetting behavior suggest increasing mobility in a silicate host rock, as sulfide liquids become more Cu-rich. Partition coefficients for copper, 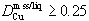 are obtained from Ni-bearing experiments with ~2 weight percent Cu and no quench phases. The equation
are obtained from Ni-bearing experiments with ~2 weight percent Cu and no quench phases. The equation
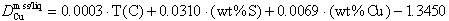
describes partitioning observed in Ni-free experiments above 1000°
C. Above 1000°
C, the Ni distribution coefficient 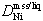 decreases with increasing temperature and/or sulfur content of the liquid.
decreases with increasing temperature and/or sulfur content of the liquid.
These results yield improved models describing the fractional crystallization of natural sulfide liquids. Major element (Fe, Ni, Cu, S) compositions of ores from the Sudbury district are shown to be entirely consistent with fractional crystallization at temperatures above 1000°
C, with the possible exception of rare samples enriched in both Ni and Cu. Sulfide liquids fractionating Ni-Fe-rich hanging wall ores at Sudbury, Ontario, must have been less Cu-rich than previously thought. At temperatures above 900°
, reduced sulfur activity in residual liquids can result in massive late-stage bornite-rich ores.
Introduction
Fe-Ni-Cu sulfide phases are important to metallurgy, meteorite studies, mantle and core geochemistry, and precious metals exploration, the focus of the present work. In the liquid state, immiscible sulfide liquids collect chalcophile metals from coexisting silicate melts (Goldschmidt, 1954). These sulfide liquids have mechanical properties very different from the silicate melts. It has been shown that many copper-nickel orebodies represent immiscible sulfide liquids segregated from their host magmas (Naldrett, 1989). Field relations and compositions of particularly Cu-rich variants of these ores suggest they result from fractional crystallization of the initial sulfide liquids, and these ores are especially interesting because of their elevated platinum group element (PGE) and gold contents. Recently Li et al. (1992) and Naldrett et al. (1994a, b) have demonstrated the need for improved phase equilibrium data in modeling the fractional crystallization of sulfide ores at Noril'sk, Siberia, and at Sudbury, Ontario; hence the present work.
The compositions relevant to magmatic sulfide ores range from 0 to 15 wt% Ni, 0-32 wt% Cu, 34-40 wt% S, with the balance Fe and trace amounts of Co, Pd, Pt, Rh, Ir, Ru, Os and Au. Iron-dominated sulfide liquids with low surface tension and low viscosity, and therefore high capillary mobility, begin to crystallize pyrrhotite (Fe0.917S) at 1190±
1°
C (Jensen, 1942). The monosulfide solid solution (mss), (Fe,Ni)1-xS, extends completely to Ni0.192S at 992°
C (Rau, 1975). Trace Cu strongly depresses the temperature of initial mss crystallization, especially at high sulfur fugacity. Intermediate solid solution (iss) is a sulfur-deficient phase ranging nearly to cubanite, CuFe2S3, at higher temperatures, and stable in the Ni-free system at least to 902°
(Dutrizac, 1976). This figure is in reasonable agreement with Merwin and Lombard's (1937, their fig. 2) observation of first melting at ca. 920°
near the CuFe2S3-FeS join, suggesting that Yund and Kullerud's (1966) value of 960°
is too high. Chalcopyrite, CuFeS2, is only stable to 882°
(Conard et al., 1980). The alloy systems (Conard et al., 1978; Chuang et al., 1984, 1986), Fe-S binary (Fernandez Guillermet et al., 1981; Chuang et al., 1985), and Ni-S binary (Sharma and Chang, 1980) have been reviewed elsewhere.
Earlier work on mss-liquid relations at 1100°
C in the Fe-Ni-S phase diagram is illustrated in Figure 1, with the present results superposed. In this work, phase relations will be plotted entirely as weight percent in cartesian coordinates. The former consideration reflects the standard expression of ore composition data, the ease of conversion to atomic proportions for Fe, Ni and Cu, and the observation that plotting arbitrary ratios of elements can lead to misleading correlations, especially when one element is at low concentration. As in Figure 3, we have retrieved numerical weight percent data manually from published ternary representations. Workers at the Geophysical Laboratory of the Carnegie Institution investigated the FeS-S join (Jensen, 1942), and the Fe-Ni-S system (reviewed by Kullerud et al., 1969). Chang and Hsieh (1986) rigorously and successfully quantified the thermodynamics of the Fe-Ni-S ternary (cf. Hsieh, 1983; Hsieh et al., 1982, 1987a,b; Conard et al., 1987). They used an associated-solution model for Fe-Ni-S liquid, coupled with a subregular solution model for the mss. We could find no previous high-temperature experimental determinations of ternary phase equilibria on the sulfur-rich side of the FeS-NiS pseudobinary join in the system Fe-Ni-S.
In the system Cu-Fe-S, Kullerud et al.'s (1969) review of phase equilibrium and DTA work has been the work of reference (cf. Cabri, 1973; Chuang, 1983). Phase equilibrium data in the Cu-Fe-Ni-S quaternary consist solely of Fleet and Pan's (1994) pioneering work on Fe-rich bulk compositions at and below 1050°
C. Here, we extend the quaternary database to higher temperatures, and provide results at lower temperatures for inter-laboratory comparison. To connect these results to the ternary systems, the Fe-Ni-S phase equilibria have been reexamined at and above 1100°
. This is the first such work to utilize the electron microprobe. Our examination of the system Fe-Cu-S similarly updates work done in the 1960's, however many more temperatures are investigated (Table 2). We believe our results, combined with existing activity data, are of a quality sufficient for the calibration of thermodynamic properties of sulfide liquids. Such models, already used in metallurgy, may have important application to magmatic sulfide petrology, particularly if they can be coupled with models describing silicate melt crystallization (e.g. Ghiorso and Sack, 1995).
Experimental Techniques
Only the barest outline of experiment and analysis technique is presented here. Space does not permit illustration or discussion of preparation or quench procedures in relation to the methods of other groups (e.g. Fleet and Pan, 1994). We also omit all discussion of microprobe analysis, particularly the choice of standards, analysis parameters, and randomness of analysis points. Furthermore, methods used to prevent oxidation are not detailed. On all of these points, we have either improved upon or duplicated the most accurate techniques used in all previous studies cited here. Persons setting out to reproduce, extend, or critically evaluate the present work are urged to obtain detailed documentation, including photographs of results, from the first author.
A quartz tube technique (Kullerud, 1971) was chosen over pressurized collapsible tube methods to ensure a rapid quench. Free space in the tubes is estimated to be 50-75% of the internal volume. Charges were heated at 1200°
C to form a sulfide melt, then suspended at the end of a glass rod in the hot-spot (±
0.7°
) of a Deltech vertical-tube furnace, at the target temperature (Table 1). All experiments were quenched in the same way, by dropping the rod exactly 34cm into a water bath to rapidly quench the run. We believe this more rapid quench, with identical rates at a given temperature, may explain minor differences between our results and those of Fleet and Pan (1994). Products were mounted with careful attention to spatial position in the tube, and analysed on the electron microprobe in the Duncan Derry laboratory, Department of Geology, University of Toronto. All materials were stored in a vacuum dessicator when not in use.
Attainment of equilibrium was inferred from these observations: (1) duplicate bulk compositions, reacted for different durations, yielded identical results; (2) distinct separation of single crystal mss and matte (liquid) always occured; (3) analyses of mss and Fe-Ni-S liquid were identical at 1 and 30 micron scales; (4) mss and liquid phases were homogeneous, optically and microanalytically (Table 2), from tube wall to core, and top to bottom; (5) single-phase results were completely consistent with multiple-phase results; (6) experience of Ebel and Sack (1989) with refractory (Zn,Fe)S, and reports by other workers (e.g. Fleet et al., 1993), indicate rapid equilibration at these near-liquidus temperatures (cf. Barton and Skinner, 1979, their fig. 7.1). Here, "identical" means analyses concur within microprobe precision.
Results and Discussion
Quenched experiments were generally similar to each other in the arrangement of materials in the tube, and their microscopic textures. In a typical quenched tube, an ingot consisting of sulfide liquid and crystalline mss was suspended above the tapered bottom of the tube, and the boundary between mss and quenched liquid was usually very sharp, and visible through the tube wall. In all but the most Cu-rich experiments, mss formed a distinct, optically homogeneous (i.e. uniform extinction in reflected light) cleavable single crystal immediately below the quenched liquid. Liquid typically crept up the walls, forming a thin, largely hollow cylinder which crystallized on quenching to an optically heterogeneous (i.e. patches with different extinction angles, but compositionally homogeneous) mosaic of microcrystalline quench mss, with evenly distributed, very fine quench iss or bornite dispersed in Cu-rich liquids. As total Cu content increased, ingot walls became thinner, wetting of tube walls was enhanced, and ingots appeared closer to the tapered ends of tubes, all indicating a decrease in surface tension of the sulfide liquid. On the other hand, in the system Fe-Ni-S, little difference in behavior was observed as Ni was increased at constant sulfur content, but high-sulfur liquids exhibited enhanced wetting behavior, and a greatly increased tendency to form vesicles.
Hemispherical voids up to 1mm diameter occurred on tube walls in the quenched liquid of both sulfur-rich and sulfur-poor experiments. Much smaller, similar voids occurred on the tube wall in the coexisting mss. Upon quenching, sulfide ingots contracted from the walls of the tubes, leaving behind a dark, thin sulfide film, as reported by Fleet and Stone (1991), and Naldrett (1969). This film was not present where voids in the quenched liquid were against the tube wall, and was thicker in experiments heated for a longer duration, and in Cu-rich experiments. The voids are interpreted to be sulfur vapor bubbles, nucleated early, and grown at the expense of smaller ones during the experiment. The quench texture is reminiscent of pores in castings at reduced-pressure (e.g. Samuel and Samuel, 1993, their fig. 16), and in more slowly quenched FeS-S mixtures (Arnold, 1971, his fig. 3).
Sulfur-rich quenched liquids appeared more like quenched foam, with hollow, domed shapes and extremely vesiculated interiors, some with septa less than 5m
m wide in polished section. Extrapolating these features to natural confining pressures, the high-S liquid compositions we measured represent natural high-sulfur liquids, which would contain dissolved sulfur equivalent to the condensed vapor seen in our experiments. Materials quenched more slowly (e.g. experiments of Arnold, 1971, with quench pyrite) show resorption of sulfur by the condensed sulfides from the vapor. No such resorption was observed in the present experiments.
Surface tension is a measure of ore liquids' tendency to infiltrate cracks and to flow easily through silicate host rocks. As S content decreased there was a greatly increased tendency of sulfide to adhere to silica glass, so that glass spalled from the tube wall at quench. This was particularly evident in Ni-free experiments, where the degree of spalling increased dramatically with decreasing total sulfur content, and with increasing wt% Cu in the final liquid. In a few Ni-free experiments (1ca, 1cb, 3cc), it was evident that sulfide liquid had "slumped" to the end of the tube, leaving crystalline mss firmly adhering to the tube wall nearer the top end. This is analogous to stress-driven separation of sulfide liquids and solids in nature. Some Cu-rich liquids showed a tendency to envelop coexisting mss, forming a thin selvage between mss and the silica tube. In the system Fe-Cu-S, experiments 3cb, 4ca and 1cc resulted in coarsely crystalline mss centered in the middle of the tube, surrounded by sulfide liquid, which was the only phase to contact the tube wall. Clearly, the total free energy of these liquids is very much reduced by contact with the silica glass. These observations suggest that as natural sulfide liquids become more Cu-rich, they have an increased tendency to leave crystalline sulfide behind, in favor of contact with fracture surfaces in silicate host rock.
The differential compressibilities of sulfide liquids have not been investigated, but the present results indicate that most sulfide liquids are less dense than the mss with which they coexist at low pressures. However, in experiments 4cb and 4cc, several very large (>1.5mm diameter) grains of mss were suspended in sulfide liquid (quenched to an iss + mss mixture homogeneous on a 30 micron scale), suggesting neutral buoyancy of equilibrium mss in these liquids at 1050°
C. Therefore it is likely that natural liquids richer in Cu, at this or lower temperatures, are more dense than the mss which crystallizes from them, if nickel is considered to partition nearly equally between the phases (cf. Fleet and Pan, 1994). Since the compressibilities of the liquids should be greater than those of the solids, pressure will increase the threshold temperature and decrease the required Cu content at which this density inversion occurs. In our experiments, Cu- and S-rich liquids contained greater abundances of metastable (quench) iss and mss than did other, identically quenched final liquids, suggesting more rapid diffusion rates in Cu- and S-rich liquids.
Final compositions of Fe-Ni-S experiments are listed in Table 2a. Crystallographic continuity, and complete compositional homogeneity of the mss bolster the conclusion that mss stable above 1000°
C suffers no change in composition at our quench rates. Occasionally, slight (<0.5 wt%) Ni enrichment was observed in quenched liquid immediately adjacent to tube walls, relative to liquid nearer the ingot core (all tubes were 3mm internal diameter, with 1mm thick walls). However, all compositional variations among random fragments of any phase were close to microprobe precision limits, and all analyses are averaged into the final tabulations (Table 2). In S-poor experiments, a metal-rich fraction separated from the liquid in a very fine, uniformly-distributed lacework. Such quench textures are common in metal-sulfide work (e.g. Fleet et al., 1993, their fig. 1), and result when one phase, dissolved in the liquid at the target temperature, "exsolves" from it extremely rapidly during the quench. We report the compositions of these phases when possible (Table 2), along with the bulk composition of the liquid obtained with a wide microprobe beam.
Results of experiments in the system Fe-Ni-Cu-S are tabulated in Table 2b. Bulk compositions with <2 wt % Cu contained liquid with no quench phases (Fig. 3). Other liquids with >2 wt% Cu contained very fine (<2m
), very evenly dispersed grains of quench intermediate solid solution (iss), a phase known to be stable only well below all the target temperatures. Such liquids also seemed to lose more sulfur to the vapor phase on quench, and exibit a more "frothy" texture, than similar Cu-free experiments. These observations suggest that Cu enhances diffusion speed in sulfide liquids. In natural systems, high pressures suppress vapor, so our results provide a minimum bound on the equilibrium sulfur content of the liquid. A maximum bound may be inferred, for any high-sulfur experiment, at the intersection of the line joining bulk composition and solid, with a line vertical from our measured liquid composition (Figs. 2, 3).
In the system Cu-Fe-S, all but one experiment exhibited exsolution, from the sulfide liquid, of very fine, anhedral mss and an iss of near-cubanite composition. As in the other experiments, all observed phases, at any scale, are reported, and all analyses of each phase are included in its average and (1s
) standard deviation (Table 2). Compositions of exsolved, host and bulk liquid phases could be obtained using narrow and broad microprobe beams. As described above, primary mss, not intergrown with any Cu-rich phase, formed in distinct textural contrast to the surrounding sulfide liquid. Several experiments contained small droplets separated from the major mass of material, but these were nearly identical in composition to the liquid in the main ingot, and are not reported in Table 2c. In experiment 4cc, a bornite-like composition, not iss, exsolved from the liquid, and quenched liquid exhibited an extremely fine-grained metallic copper coating on free surfaces. Ni-bearing, low-S experiment fp110, also with low-sulfur at 1050°
C, exhibitted a nearly identical quench texture. Metallic copper is a known low-temperature exsolution product of bornite solid solution (Merwin and Lombard, 1937).
Phase Diagrams
In the Fe-Ni-S ternary, the present results confirm Chang and Hsieh's (1986) calculated stability field for mss at 1100°
C (Figs. 1, 2). As sulfur saturation is approached, at the "nose" of the mss field, the liquid becomes more Ni-rich than previously thought. On the high-sulfur side of this region, the bulk compositions necessary for stability of both mss and liquid at very low pressure no longer fall on the tie-lines between them. Here (above about 39 wt% S in this T-X region) excess sulfur must be present to fill unavoidable free space in the silica tube with vapor. Experiments with S > ~39% by weight contained prominent droplets of quenched sulfur vapor, but those with lower S content contained only a fine "mist" of tiny condensed S droplets. Some small fraction of the final sulfur vapor in sulfur-rich experiments must be exsolved from the liquid during the quench in the high-S experiments, yet no significant decreases in sulfur concentration were detected in microprobe traverses toward voids in the sulfide liquid. In ore-forming systems, ambient pressures would suppress this vapor phase, and any free sulfur would combine readily with available metals (cf. Naldrett and Gasparrini, 1971), thereby buffering the sulfur fugacity where liquids are in close proximity to host silicates. The position of the high-sulfur liquidus is, however, of great interest in the thermodynamic modeling of the system. It can be seen that the present results represent minimum bounds on the sulfur content of liquids coexisting with mss on the high-sulfur side (Figs. 2, 4).
The Fe-Ni-S phase diagrams of reference (Hsieh et al., 1982; Chang and Hsieh, 1986) are constructed from a combination of several thermochemical models. Hsieh's (1980) model for mss was calibrated from gravimetric determinations of sulfur activity in mss (Fe,Ni1-x)S obtained at T£
900°
C. Chuang et al.'s (1985) model for Fe-S liquids poorly reproduces the sulfur activity data upon which it is based (their fig. 2; cf.-Chuang, 1983, p.256), most of which is for metal-rich liquids. It should be possible to modify the model of Hsieh et al. (1987a,b) to address the new phase equilibrium data. Such a modification would be more readily obtained using an associated solution formulation for the liquid, or a two-sublattice model, in contrast to a theoretically equivalent subregular solution model, since only solutions for liquids in the FeS-NiS-S pseudoternary appear to be in question. Thermodynamic modeling of the sulfur-saturated portions of these systems, addressing low-pressure data, must include a rigorous description of the vapor properties at high temperatures (Mills, 1974). Textures indicate that the vapor mixes intimately with the sulfide liquid at high temperatures.
Effects of adding <3 wt% Cu to the system Fe-Ni-S at 1100�C are illustrated in Figure 3. Such liquids represent the earliest stages of fractional crystallization of magmatic ore . Comparison with Figure 2 shows the mss stability field shrinks, becoming less S-rich, and less Ni-rich upon the addition of trace Cu at constant temperature. In high-S, low-Ni experiments, the measured S content of the liquid decreases markedly with Cu-enrichment, yet the bulk composition necessary for stabilization of observable liquid is much lower in S for the Cu-bearing experiments. Quenching techniques were identical for all experiments, so relative changes in the distribution of sulfur are real, or else record a profound, Cu-dependent difference in the retention of S by the liquids on quenching.
Results of Ni-free experiments at 1100�C are compared to the phase diagram of Kullerud et al. (1969), and to results in the Fe-S binary, in Figure 4a. By 1050�C (Fig. 4b), the sulfide liquid (exp. 4cb) can exceed the Cu content of the Fe-rich tip of the intermediate solid solution (iss), near cubanite, CuFe2S3. At low total sulfur (low sulfur fugacity in the closed silica tube) bornite becomes a metastable (quench) phase, suggesting that Cu2S is an important complex in the sulfide liquid. This suggests a mechanism for formation of massive bornite ores by such liquids, if sulfur fugacity is depressed, for example by the addition of metal, reduction, or the escape of an oxysulfide phase. As noted above, liquids in the system Fe-Ni-S have been modeled with some success as solutions dominated by FeS and NiS species. If such an approach is to be extended to the system of practical interest, both CuS and Cu2S must be considered as species in the liquid. Equilibrium of these species in sulfide liquid would constitute an internal sulfur-fugacity buffer, perhaps controlling general trends in the compositions of massive ores from Noril'sk and Sudbury, and specifically their bulk sulfur content.
Partition coefficients
Major and trace elements exhibit complex partitioning behavior between magmatic sulfide liquids and their early crystallizing phases. As sulfur content increases, Ni partitions more strongly into the liquid, relative to the coexisting mss, in the Cu-free system at 1100°
C (Fig. 5a). As temperature decreases, more Ni enters the mss, from liquids with the same sulfur content. Data for Cu-bearing experiments shows similar variation in DNi, with increasing S driving Ni out of the sulfide liquid (Fig. 5b). As the Cu content of the liquid increases, and temperature decreases, it is likely that DNi becomes greater than 1.0, and Ni begins to partition into the mss. A reversal (DNi >1.0) at lower temperatures would be consistent with bulk compositions of the deep copper ores at Strathcona, which are poorer in Ni than the footwall copper ores above them (Figs. 6a, 7). The latter have been interpreted by Naldrett et al. (1994a) to be a mixture of trapped sulfide liquid and mss, less fractionated precursors to the sulfide liquid which formed the deep copper ore.
Partition coefficients for Cu also decrease with decreasing S in the liquid (Fig. 5c). A value of 0.1 for the Nernst distribution coefficient 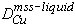 of copper between mss and sulfide liquid has frequently been used to model sulfide liquid fractionation (e.g. Naldrett et al., 1994a,b). The present results indicate that DCu is greater than 0.25 for Cu-poor liquids above 1100°
C, where sulfide ore liquids begin to crystallize mss (Naldrett, 1989). D-values decrease as the liquids become more Cu-rich, and temperature decreases (Fig. 5d). The observed variation of DCu does not have a strong effect on qualitative consideration of the processes resulting in ore formation, however quantitative approaches to exploration require the most realistic values of DCu possible. Simple linear approximations for DCu and DNi are presented below.
of copper between mss and sulfide liquid has frequently been used to model sulfide liquid fractionation (e.g. Naldrett et al., 1994a,b). The present results indicate that DCu is greater than 0.25 for Cu-poor liquids above 1100°
C, where sulfide ore liquids begin to crystallize mss (Naldrett, 1989). D-values decrease as the liquids become more Cu-rich, and temperature decreases (Fig. 5d). The observed variation of DCu does not have a strong effect on qualitative consideration of the processes resulting in ore formation, however quantitative approaches to exploration require the most realistic values of DCu possible. Simple linear approximations for DCu and DNi are presented below.
The distribution coefficient itself derives from an assumption of Henry's Law behavior (Anderson and Crerar, 1993), applied to the equilibrium between two phases (e.g. mss and liquid), where the thermodynamic activity of a species (e.g. Cu) must be the same in each phase. Under this assumption, the value of D is a constant, or may show slight temperature dependence, equivalent to assuming that the ratio of the activity coefficients in the two phases is constant. The assumption is valid in the dilute limit, as is the approximation that the concentration ratio (wt % or ppm) of the species is equivalent to its mole fraction ratio. For the case at hand, this reasoning can be expressed as
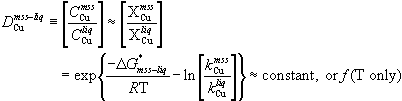 (1)
(1)
where C are concentrations, X are mole fractions, 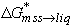 is the (molar) Gibbs free energy change of the system as (one mole of) Cu is transferred from mss to liquid, and k are the Henry's law constants of Cu in each phase.
is the (molar) Gibbs free energy change of the system as (one mole of) Cu is transferred from mss to liquid, and k are the Henry's law constants of Cu in each phase.
The similar atomic weights of Fe, Ni and Cu validate the approximation that concentration equals mole fraction, even for major elements. However, several lines of evidence indicate that the assumptions behind the constancy of 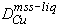 break down as
break down as 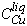 increases. In experiments, the Cu-rich phase iss is observed to nucleate extremely rapidly during quench from liquids with >3 wt% Cu, but not from less Cu-rich sulfide liquids (Table 2). Further, the composition of exsolved iss, from identically quenched experiments, appears to vary with liquid composition. Interfacial energies of metals and mattes (Utigard, 1993; Ip and Toguri, 1993), and qualitative observations of the present experimental textures, also suggest significant variation in mechanical properties of sulfide liquids, as
increases. In experiments, the Cu-rich phase iss is observed to nucleate extremely rapidly during quench from liquids with >3 wt% Cu, but not from less Cu-rich sulfide liquids (Table 2). Further, the composition of exsolved iss, from identically quenched experiments, appears to vary with liquid composition. Interfacial energies of metals and mattes (Utigard, 1993; Ip and Toguri, 1993), and qualitative observations of the present experimental textures, also suggest significant variation in mechanical properties of sulfide liquids, as 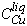 increases. Furthermore, the topology of the Cu-S binary is quite unlike those of Fe-S and Ni-S. The present database on the Fe-Ni-Cu-S quaternary confirms that Cu substitution has a very significant effect on the stability of mss, as does sulfur activity. These effects are manifested in a significant depression of the melting temperature of mss, narrowing of the mss stability field, and its dip away from the sulfur apex to more S-poor compositions, as
increases. Furthermore, the topology of the Cu-S binary is quite unlike those of Fe-S and Ni-S. The present database on the Fe-Ni-Cu-S quaternary confirms that Cu substitution has a very significant effect on the stability of mss, as does sulfur activity. These effects are manifested in a significant depression of the melting temperature of mss, narrowing of the mss stability field, and its dip away from the sulfur apex to more S-poor compositions, as 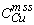 increases. These non-ideal phenomena in mss and sulfide liquid make it unlikely that a constant value for
increases. These non-ideal phenomena in mss and sulfide liquid make it unlikely that a constant value for 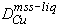 will apply to fractional crystallization, particularly as Cu becomes a major component of the liquid, sulfur activity varies, and temperature decreases.
will apply to fractional crystallization, particularly as Cu becomes a major component of the liquid, sulfur activity varies, and temperature decreases.
Application
In the absence of a rigorous model for sulfide liquid properties (see, however, Kress, 1994), it is reasonable to account empirically for changes in DCu as 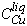 increases beyond 2 wt% in the composition range of interest. We have seen that the value of DCu decreases, that is, more Cu remains in the liquid, as temperature decreases, bulk composition of Cu and/or Ni increases, or sulfur content decreases (Fig. 5). Of these variables, temperature and S and Cu content are assumed to dominate natural fractional crystallization processes, since little variation is seen in the Ni content of the ores. Simple multiple regression results are presented here with the caveat that they frequently yield specious results if extrapolated beyond the range of the source data, and should be used with great caution. Such calculations for DCu (1050-1150°
; Ni-free) and DNi (900-1180°
; Ni in liquid < 10wt%) result in:
increases beyond 2 wt% in the composition range of interest. We have seen that the value of DCu decreases, that is, more Cu remains in the liquid, as temperature decreases, bulk composition of Cu and/or Ni increases, or sulfur content decreases (Fig. 5). Of these variables, temperature and S and Cu content are assumed to dominate natural fractional crystallization processes, since little variation is seen in the Ni content of the ores. Simple multiple regression results are presented here with the caveat that they frequently yield specious results if extrapolated beyond the range of the source data, and should be used with great caution. Such calculations for DCu (1050-1150°
; Ni-free) and DNi (900-1180°
; Ni in liquid < 10wt%) result in:
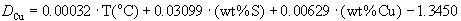 (2)
(2)
Cu: n=12; multiple r2=0.90; std. error=0.02; data of Table 2c
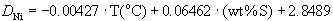 (3)
(3)
Ni: n=43; multiple r2=0.71; std. error=0.15; data of Table 2a and 2b, also Fleet and Pan (1994).
Models for the fractional crystallization of ore liquids also require assumption of a plausible initial liquid composition, based on the composition and amount of silicate magma with which the sulfide liquid interacted before it segregated (cf. Zientek et al. 1994; Naldrett et al., 1994a). Sulfide/silicate partition coefficients are thought to be roughly equal for Cu and Ni, so Cu/Ni ratios of initial sulfide liquids should mimic ratios in the source silicate magma. At Strathcona, this ratio has been thought to be nearly 1:1. But consider that early fractionation produced an mss, with no trapped sulfide liquid, represented by the bulk composition of the hanging wall ores with low Ni and Cu content (Li et al., 1992, Table 3). To have crystallized this mss with an initial DCu of 0.25, the initial sulfide liquid cannot have contained more than about 2 weight % Cu. However, Pessaran's (1993; cf. Naldrett et al., 1994a, Table 12.1) composite samples, weighted toward hanging wall ore, contain up to 7.8% nickel.
It is unlikely that the entirety of major element variation in ores can be ascribed to any single, simple process. However, the major element variations in this case are quite consistent with fractional crystallization. Given accurate partition coefficients, and a plausible estimate of the initial sulfide liquid composition, it is a relatively straightforward exercise to calculate the path of crystallization of the liquid, using Rayleigh fractionation equations. Such paths are best illustrated by examination of pairs of elements, one with an affinity for mss, the other for sulfide liquid, using methods demonstrated by Li and Naldrett (1995). The search for fugitive, Cu-rich liquids can be aided by comparison of such paths with field data, and contouring of the sampled area in terms of the proportions of primary liquid and mss represented in the ore. In Figure 6, a crystallization path for Strathcona ores is presented, which makes use of varying D values, in contrast to the constant values assumed by previous workers.
With the new partition coefficient data, Ni and Cu can be compared directly with some accuracy (Fig. 6a). However, the trace PGE with an affinity for the mss (e.g. Rh) have been considered more useful than Ni for modeling, because their D values can be assumed constant. Figure 6b compares the Sudbury ores of Figure 6a with predicted fractionation of copper and rhodium, an element very compatible with mss (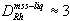 , Fleet et al. 1993). In these calculations, an initial sulfide liquid of 0.6 ppm Rh, 1.5 wt% Cu, and 5% Ni is considered, nearly sufficient to produce the mss represented by the low-Cu hanging wall ores, assuming that they contained no trapped liquid. Use of composition-dependent D values requires an iterative calculation procedure. On each of 95 iterations, 1% of initial liquid crystallizes as mss, and temperature decreases 1.5°
from 1100°
C initially. The parameters DCu and DNi follow the regression above, and DRh is set to 3 throughout. Sulfur content of the liquid is assumed to decrease according to
, Fleet et al. 1993). In these calculations, an initial sulfide liquid of 0.6 ppm Rh, 1.5 wt% Cu, and 5% Ni is considered, nearly sufficient to produce the mss represented by the low-Cu hanging wall ores, assuming that they contained no trapped liquid. Use of composition-dependent D values requires an iterative calculation procedure. On each of 95 iterations, 1% of initial liquid crystallizes as mss, and temperature decreases 1.5°
from 1100°
C initially. The parameters DCu and DNi follow the regression above, and DRh is set to 3 throughout. Sulfur content of the liquid is assumed to decrease according to 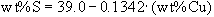 , consistent with the paths of Sudbury and Noril'sk ores. Some contact ore compositions do not fall inside the mss-liquid fractionation envelopes of Figure 6, appearing to be more copper-rich than the postulated initial sulfide liquid. However (arrow B), only a small quantity of a more highly fractionated liquid could, migrating into the contact ore, produce these Cu-rich ores. Such a liquid, partially crystallizing within the hanging wall, could pass through and alter early fractionates crystallized in the footwall. Alternatively, Cu could have been added to these early ores by post-ore alteration processes, such as those observable at the Whistle Pit on the northeast range. Regardless of the detailed scenario invoked to explain particular local compositions, comparison of the overall trends of these ores with the results of our experiments (Fig. 7) illustrates their consistency with a fractional crystallization origin.
, consistent with the paths of Sudbury and Noril'sk ores. Some contact ore compositions do not fall inside the mss-liquid fractionation envelopes of Figure 6, appearing to be more copper-rich than the postulated initial sulfide liquid. However (arrow B), only a small quantity of a more highly fractionated liquid could, migrating into the contact ore, produce these Cu-rich ores. Such a liquid, partially crystallizing within the hanging wall, could pass through and alter early fractionates crystallized in the footwall. Alternatively, Cu could have been added to these early ores by post-ore alteration processes, such as those observable at the Whistle Pit on the northeast range. Regardless of the detailed scenario invoked to explain particular local compositions, comparison of the overall trends of these ores with the results of our experiments (Fig. 7) illustrates their consistency with a fractional crystallization origin.
Conclusions
1. New data suggest a need for revision of the Fe-Ni-S and Fe-Cu-S phase diagrams of current reference, Hsieh et al. (1982) and Kullerud et al. (1969).
2. Distribution coefficients for major elements Ni, Cu, and S between sulfide liquids and mss vary with composition, temperature and sulfur activity. Simple empirical corrections suffice to model fractional crystallization of sulfide liquids in a first approximation.
3. 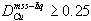 in the composition range relevant to fractional crystallization of many magmatic sulfide ores. DCu decreases with decreasing temperature and sulfur fugacity. The initial sulfide liquid from which the Cu-poor hanging wall ores at Strathcona fractionated could not have been as Cu-rich as has been heretofore thought.
in the composition range relevant to fractional crystallization of many magmatic sulfide ores. DCu decreases with decreasing temperature and sulfur fugacity. The initial sulfide liquid from which the Cu-poor hanging wall ores at Strathcona fractionated could not have been as Cu-rich as has been heretofore thought.
4. Modeling of composition variation can be improved by the use of composition-dependent distribution coefficients for major elements. Composition trends for Sudbury ores are entirely consistent with a fractional crystallization origin.
5. Increase of Cu content in sulfide liquids dramatically affects their mechanical properties, decreasing viscosity and surface tension. In crustal pressure regimes, early mss probably sinks in a low-Cu, high-S liquid. As liquid becomes more metal-rich, later, more Cu-rich mss should attain neutral buoyancy. Late liquids rich in Cu and trace elements are more dense than the mss they crystallize, and more mobile than the earlier liquids.
6. Crystallization paths bypassing the intermediate solid solution (iss) and resulting in bornite stability are possible at 1050°
C, if sulfur is removed, or metals added to the system. Preferred paths of ores and experimental sulfide liquids suggest Cu2S complexes are important in these liquids, in addition to FeS, NiS and CuS.
7. Better understanding of fractional crystallization of sulfide liquids in nature would follow from studies of their densities and dynamic properties. Further phase equilibrium and DTA work should focus on the deeper interior of the Fe-Ni-Cu-S quaternary. Trace elements including semimetals (As, Sb, etc.), and oxygen, may influence phase relations differently in different composition regions. Careful experimental work in all these areas would be useful in the modeling of natural fractional crystallization, and in metallurgists' modeling of smelting processes.
Acknowledgments
We thank Dr. Grant Henderson for use of the second furnace. The collaborative support of INCO, Falconbridge Ltd., and the National Science and Engineering Research Council of Canada is greatly appreciated.
References
Anderson, G. M., and Crerar, A., 1993, Thermodynamics in geochemistry: The equilibrium model. New York, Oxford University Press, 588 p.
Arnold, R. G. 1971, Evidence for liquid immiscibility in the system FeS-S: Economic Geology, v. 66, p.1121-1130.
Barton, P. B., Jr., and Skinner, B. J., 1979, Sulfide mineral stabilities. In Barnes, H. L. ed., Geochemistry of Hydrothermal Ore Deposits, 2nd ed., Wiley Interscience, New York, p. 278-403.
Burgmann, W., Urbain, G., and Frohberg, M. G., 1968, Contribution à l'étude du système fer-soufre limité au domaine du mono-sulfure de fer (pyrrhotine): Mémoires Scientifiques de la Revue de Métallurgie, v. 65, p.567-578.
Cabri, L., 1973, New data on phase relations in the Cu-Fe-S system: Economic Geology, v. 68, p.443-454.
Chang, Y. A., and Hsieh, K-C., 1986, Thermochemical description of the ternary iron-nickel-sulphur system. In Nickel Metallurgy: volume 1: Extraction and Refining of Nickel, E. Ozberk and S.W. Marcuson, eds., Proceedings of the 25th annual conference of metallurgists, Canadian Institute of Mining and Metallurgy, p.248-277.
Chuang, Y.-Y., 1983, The thermodynamics and phase equilibria of the copper-nickel-iron-sulfur quaternary Ssystem and its subsystems. Unpublished Ph.D. Dissertation, Madison, Wisconsin, The University of Wisconsin - Madison, 325 p.
Chuang, Y.-Y., Paik, J., Pérepezko, J. H., and Chang, Y. A., 1984, Thermodynamic analysis of the iron-copper system 1: the stable and metastable phase equilibria: Metallurgical Transactions A, v. 15A, p.1921-1930.
Chuang, Y.-Y., Hsieh, K.-C., and Chang, Y. A., 1985, Thermodynamics and phase relationships of transition metal-sulfur systems: Part V. A reevaluation of the Fe-S system using an associated solution model for the liquid phase: Metallurgical Transactions B, v. 16B, p.277-285.
Chuang, Y.-Y., Hsieh, K.-C., and Chang, Y. A., 1986, A thermodynamic analysis of the phase equilibria of the Fe-Ni system above 1200 K: Metallurgical Transactions A, v. 17A, p.1373-1380.
Conard, B. R., McAneney, T., and Sridhar, R., 1978, Thermodynamics of iron-nickel alloys by mass spectrometry: Metallurgical Transactions B, v. 9B, p.463-468.
Conard, B. R., Sridhar, R., and Warner, J. S., 1980, High-temperature thermodynamic properties of chalcopyrite: Journal of Chemical Thermodynamics, v. 12, p. 817-833.
Conard, B. R., Meyer, G. A., Timberg, L., Warner, J. S., and Hynek, P., 1987, Thermodynamic activities of components in homogeneous Ni-Fe-S mattes at 1473-1673 K: Canadian Metallurgical Quarterly, v. 26, p.299-309.
Dutrizac, J.E., 1976, Reactions in cubanite and chalcopyrite: Canadian Mineralogist, v. 14, p.172-181.
Ebel, D. S., and Sack, R. O., 1989, Ag-Cu and As-Sb exchange energies in tetrahedrite-tennantite fahlore: Geochimica et Cosmochimica, v. 53, p. 2301-2309.
Fernandez Guillermet, A., Hillert, M., Jansson, B., and Sundman, B., 1981, An assessment of the Fe-S system using a two-sublattice model for the liquid phase: Metallurgical Transactions B, v. 12, p.745-754.
Fleet, M. E., and Stone, W. E., 1991, Partitioning of platinum-group elements in the Fe-Ni-S system and their fractionation in nature: Geochimica et Cosmochimica Acta, v. 55, p.245-253.
Fleet, M. E., and Pan, Y., 1994, Fractional crystallization of anhydrous sulfide liquid in the system Fe-Ni-Cu-S, with application to magmatic sulfide deposits: Geochimica et Cosmochimica Acta, v. 58, p.3369-3377.
Fleet, M. E., Chryssoulis, S. L., Stone, W. E., and Weisener, C.G., 1993, Partitioning of platinum-group elements and Au in the Fe-Ni-Cu-S system: experiments on the fractional crystallization of sulfide melt: Contributions to Mineralogy and Petrology, v. 115, p.36-44.
Ghiorso, M. S., and Sack, R. O., 1995, Chemical mass transfer in magmatic processes. IV. A revised and internally consistent thermodynamic model for the interpolation and extrapolation of liquid-solid equilibria in magmatic systems at elevated temperatures and pressures: Contributions to Mineralogy and Petrology, v. 119, p.197-212.
Goldschmidt, V. M., 1954, Geochemistry. Clarendon Press, Oxford, United Kingdom.
Hsieh, K.-C., 1980, A study of the thermodynamics and phase relationships in the Fe-Ni-S system. Unpublished Master of Science thesis, Milwaukee, Wisconsin, The University of Wisconsin - Milwaukee, 78 p.
Hsieh, K.-C., 1983, The thermodynamics and phase equilibria of the iron-nickel-sulfur-oxygen system. Unpublished Ph.D. Dissertation, Madison, Wisconsin, The University of Wisconsin - Madison, 170 p.
Hsieh, K.-C., Chang, Y.A., and Zhong, T., 1982, The Fe-Ni-S system above 700�C (iron-nickel-sulfur): Bulletin of Alloy Phase Diagrams, v. 3, p.165-172.
Hsieh, K.-C., Vlach, K. C., and Chang, Y. A., 1987a, The Fe-Ni-S system I. A thermodynamic analysis of the phase equilibria and calculation of the phase diagram from 1173 to 1623 K: High Temperature Science, v. 23, p.17-37.
Hsieh, K.-C., Schmid, R., and Chang, Y. A., 1987b, The Fe-Ni-S system II. A thermodynamic model for the ternary monosulfide phase with the nickel arsenide structure: High Temperature Science, v. 23, p.39-52.
Ip, S. W., and Toguri, J. M., 1993, Surface and interfacial tension of the Ni-Fe-S, Ni-Cu-S, and fayalite slag systems: Metallurgical Transactions B, v. 24, p.657-668.
Jensen, E., 1942, Pyrrhotite: melting relations and composition: American Journal of Science, v. 240, p.695-709.
Kress, V., 1994, Preliminary solution model for Fe-Ni-S-O liquids (abstract): EOS, v. 75, p.694.
Kullerud, G. 1971. Experimental techniques in dry sulfide research. In Ulmer, G. C. ed., Research Techniques for High Pressure and High Temperature, Springer-Verlag, Heidelberg, pp. 289-315.
Kullerud, G., Yund, R. A., and Moh, G. H., 1969, Phase relations in the Cu-Fe-S, Cu-Ni-S and Fe-Ni-S systems. In Wilson, H. D. B. ed., Magmatic Ore Deposits, Economic Geology Publishing Co., Lancaster, Pennsylvania, p.323-343.
Li, C., and Naldrett, A. J., 1995, A numerical model for the compositional variations of Sudbury sulfide ores and its application to exploration: Economic Geology, v. 89, p.1599-1607.
Li, C., Naldrett, A. J., Coats, G. J. A., and Johannessen, P., 1992, Platinum, palladium, gold and copper-rich stringers at the Strathcona Mine, Sudbury: Their enrichment by fractionation of a sulfide liquid: Economic Geology, v. 87, p.1584-1598.
Merwin, H. E., and Lombard, R. H., 1937, The system, Cu-Fe-S.: Economic Geology, v. 87, p.203-284.
Mills, K. C., 1974, Thermodynamic data for inorganic sulphides, selenides and tellurides. London, Butterworths, 845 p.
Naldrett, A. J., 1969, A portion of the Fe-S-O system and its application to sulfide ore magmas: Journal of Petrology, v. 10, p.171-201.
Naldrett, A. J., 1989, Magmatic sulfide deposits. Oxford University Press, New York, 186 p.
Naldrett, A. J. and Gasparrini, E. L., 1971, Archean nickel sulfide deposits in Canada: Their classification, geological setting and genesis with some suggestions as to exploration: Geological Society of Australia, Special Publication No. 3, p.201-226.
Naldrett, A. J., Innes, D. G., Sowa, J., and Gorton, M., 1982, Compositional variations within and between five Sudbury ore deposits: Economic Geology, v. 77, p.1519-1534.
Naldrett, A. J., Pessaran, R., Asif, M., and Li, C., 1994a, Compositional variation in the Sudbury ores and prediction of the proximity of footwall copper-PGE orebodies. Proceedings of the Sudbury-Noril'sk Symposium, Ontario Geological Survey Special Volume 5, p. 133-143.
Naldrett, A. J., Asif, M., Gorbachev, N. S., Kunilov, V. E., Stekhin, A. I., Fedorenko, V. A., and Lightfoot, P. C., 1994b, The composition of the Ni-Cu ores of the Oktyabr'sky Deposit, Noril'sk Region. Proceedings of the Sudbury-Noril'sk Symposium, Ontario Geological Survey Special Volume 5, p. 357-372.
Pessaran, A., 1993, Compositional variation in sudbury ores and proximity of footwall copper-PGE ore bodies. Unpublished Master of Science thesis, Toronto, Ontario, University of Toronto.
Rau, H., 1975, Range of homogeneity and defect interaction in high temperature nickel sulfide Ni1-xS. Journal of the Physics and Chemistry of Solids, v. 36, p.1199-1204.
Sharma, R. C. and Chang, Y. A., 1980, Thermodynamics and phase relationships of transition metal-sulfur systems: Part IV. Thermodynamic properties of the Ni-S liquid phase and the calculation of the Ni-S phase diagram. Metallurgical Transactions B, v. 11B, p.139-146.
Samuel, A. M., and Samuel, F. H., 1993, The reduced pressure test as a measuring tool in the evaluation of porosity/hydrogen content in Al-7 wt pct Si-10 vol pct SiC(p) metal matrix composite. Metallurgical Transactions A, v. 24A, p.1857-1867.
Utigard, T., 1993, Surface and interfacial energies of metals. Zeitschrift für Metallkunde, v. 84, p.792-795.
Yund, R. A., and Kullerud, G., 1966, Thermal stability of assemblages in the Cu-Fe-S system. Journal of Petrology, v. 7, p.454-488.
Zientek, M. L., Likhachev, A. P., Kunilov, V. E., Barnes, S.-J., Meier, A. L., Carlson, R. R., Briggs, P. H., Fries, T. L., and Adrian, B. M., 1994, Cumulus processes and the composition of magmatic ore deposits: examples from the Talnakh District, Russia. Proceedings of the Sudbury-Noril'sk Symposium, Ontario Geological Survey Special Volume 5, p. 373-392.
![]() are obtained from Ni-bearing experiments with ~2 weight percent Cu and no quench phases. The equation
are obtained from Ni-bearing experiments with ~2 weight percent Cu and no quench phases. The equation![]()
![]() decreases with increasing temperature and/or sulfur content of the liquid.
decreases with increasing temperature and/or sulfur content of the liquid.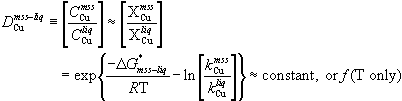 (1)
(1) The University of Chicago
The University of Chicago Department of the Geophysical Sciences at the University of Chicago
Department of the Geophysical Sciences at the University of Chicago home page.
home page.