Denton S. Ebel

Department of Geophysical Sciences, University of Chicago, Chicago, Illinois.

Abstract. Some portion of the interstellar dust entering the heliosphere is a refractory (Ca-Al-Ti-Mg-Si-Fe-Ni-Cr-Co-rich) component either condensed at high temperature from stellar outflows or formed in the interstellar medium (ISM). Condensation sequences for T>1100 K, assuming chemical equilibrium, are calculated for stellar outflow gas having (1) solar composition at various P^tot; (2) compositions approaching C/O=0.9, otherwise solar; (3) metallicities reduced by Z/Z_o=0.10; and (4) metallicities enhanced by added dust components. Calculated depletions are relatively insensitive to these excursions from the canonical "cosmic" abundances. The intragroup similarities of depletions observed for the element groups (Ca-Ti), (Fe-Ni-Cr-Co), and (Mg-Si) reflect the dominant mineralogy calculated for stardust: Ti- and Ca-aluminate phases, metal alloy, and Mg₂SiO₄ (Mg-olivine). This result suggests that the bulk of the refractory component of ISM dust was condensed in stellar environments.

Ó American Geophysical Union.

To be published in Journal of Geophysical Research - Space Physics, 1999.

There is general agreement that stellar environments are the sources of the refractory nuclei of interstellar dust particles [e.g., Jenkins, 1987]. This component is dubbed "stardust" because most of it forms around and/or in the outflows of O-rich and C-rich asymptotic giant branch (AGB) stars and is injected into the interstellar medium (ISM) by stellar winds. The remainder of the dust material must be either (1) more stardust, also from stellar environments, or (2) material accreted to the nuclei from the ISM [Snow, 1975; L.J. Allamandola et al., Evolution of interstellar ices, submitted to The Origin and Composition of Cometary Material, Space Sciences Series of ISSI, vol. 8, 1999], probably in dark clouds which are self-shielded from destructive forces [Seab, 1987; Jenkins, 1987]. This accreted component must be dominant if, in fact, stardust is destroyed in the ISM on a rapid timescale, relative to its injection [Tielens, 1998]. Grain material formed in the ISM is, however [Seab, 1987, p. 492], "likely to differ significantly from the high-temperature condensates formed in cool stars and supernova ejecta." Constraints on initial stardust composition might therefore be useful in discerning the composition and modeling the formation of the accreted ISM dust component. In this paper I will briefly explore equilibrium mineral condensation sequences for some variations on the canonical "solar" bulk composition, and I will discuss the results in terms of the observed element depletions (i.e., amounts not seen in the gas phase) for the z Ophiuchi line of sight [Jenkins, 1987]. The importance of metallic Fe in stellar condensates will be illustrated, perhaps reducing the problematically high amount of Si required by extant dust models [Snow and Witt, 1996].

The solar abundances of the elements [Anders and Grevesse, 1989] have until recently been accepted as a reasonable reference "cosmic" bulk composition for the ISM. Numerous ad hoc variations on these reference elemental abundances can be imagined. Here condensation of a gas of solar composition is revisited, the general effects of total pressure are illustrated, and several plausible vectors of variation of the bulk composition are pursued. These are the C/O ratio, a decrease in metallicity (Z/Z_o<1.0), and an increase in metallicity by the addition of two realistic types of dust component. Condensation sequences are calculated for the 23 elements given in Table 1, for a variety of bulk composition variations about the solar reference.

At least some ISM dust grains are TiC, SiC, graphite, and microdiamonds [Bernatowicz at al., 1991]; Al₂O₃ (corundum) and MgAl₂O₄ (spinel) [Nittler, 1997]; and Fe-Ni alloy [Bernatowicz et al., 1999]. The canonical solar composition (C/O~0.42) ensures partial pressures of oxygen far too high for graphite and SiC grains to form or even survive, hence carbon-rich (C/O>1) AGB stars are thought to have been the sources for most of the "mainstream" C-rich grains which survived the early solar nebula and persist in meteorites, with the rest coming from supernovae [Wooden, 1997]. In the present work, the effect of the C/O ratio is explored by varying C while holding all other elements at solar ratios.

Another vector of variation from the solar reference is metallicity. Mathis [1996], Snow and Witt [1996], and Meyer [1997] have argued that a composition of subsolar metallicity, similar to that in B stars, is a more appropriate reference composition for interstellar matter [cf. Cardelli et al., 1996]. In these compositions all elements except H and He are reduced by a factor Z/Z_o=0.70 (or less) from their solar abundances. Here an extreme scenario of Z/Z_o=0.10 is explored.

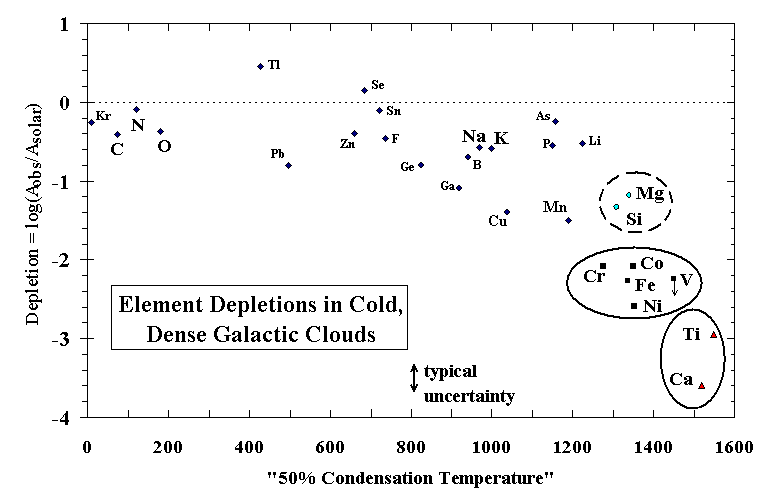
It is possible that conditions exist where stellar outflows are supplied by reservoirs having a metallicity greater than that of a gas of solar composition [e.g., Shu et al., 1994]. In such a scenario, outflow vapor enriched in precondensed dust, relative to a vapor of solar composition [Ebel and Grossman, 1998], might condense to form grains which are injected into the ISM. Two plausible dust components are investigated here. The composition of "C1 dust" is taken as the C1 chondrite Orgueil [Anders and Grevesse, 1989]. The composition of a hypothetical "ISM dust" is derived by setting the amount of each element to the fraction that it is observed to be depleted, relative to solar composition, in the cold, dense clouds toward z Oph (Figure 1). Composition for a dust enrichment n is calculated by adding (n-1) units of dust to the solar composition, both normalized to Si=10⁶ atoms.

Many workers in cosmochemistry have performed condensation calculations, including Larimer and Anders [1967], Lewis [1972], Grossman [1972], and Yoneda and Grossman [1995], on solar compositions; Lodders and Fegley [1995] and Sharp and Wasserburg [1995], on C-rich systems; and Lattimer et al. [1978] on supernova ejecta. All of these calculations have strengths and weaknesses, in both thermodynamic data and calculation algorithms, but, to first order, yield similar results. The condensation code used here is described by D.S. Ebel and L. Grossman (Condensation in dust-enriched systems, submitted to Geochimica et Cosmichimica Acta, 1998; herinafter referred to as Ebel and Grossman, submitted manuscript, 1998), and D.S. Ebel et al. (Gibbs energy minimization in gas + liquid + solid systems, submitted to Journal of Computational Chemistry, 1999). For a given bulk composition A, at fixed temperature T and total pressure P^tot, matter is apportioned between gas, liquid and solid phases, so that the chemical potential energy, the Gibbs free energy G=f(T, P^tot, A), is minimized. The assumption of chemical equilibrium is necessary, given the dearth of constraints regarding nucleation, growth, and reaction rates, diffusivities, and other properties of condensed matter at nebular conditions. It is therefore implicitly assumed that the mean free paths of atoms and molecules in the gas are short relative to cooling or expansion timescales, because densities are very high relative to the ISM. For example, at 1500 K and P^tot = 10³ dyn/cm² (1 bar = 10⁶ dyn/cm²), 1 mol of elements with solar abundance ratios has condensed ~10^-6 mol of atoms as solids, with the remaining atoms forming 0.54 mol of gaseous species occupying 6.8x10⁷ cm³, for a density of ~5x1015 molecules per cm³. It is assumed during the calculation that all condensed material is available for reaction with the gas. The sizes and shapes of grains are problems of chemical kinetics and the surface free energies of grains, which are not addressed in this work.

The elements in the gas phase are speciated among ~370 ideal gas species, with most data from the Joint Army-Navy-Air Force (JANAF) tables [Chase et al., 1985], at T£ 2400 K. Ionization of gas is not expected to be appreciable at these temperatures, and no ionic species are included in the calculation. Data for pure solids and liquids are taken from sources given by Ebel and Grossman (submitted manuscript, 1998). A strength of the current calculation engine is the inclusion of models for mineral solid solutions and a model for silicate liquid [Ghiorso and Sack, 1995], which are consistent with each other and tested against many laboratory and natural equilibrium assemblages. Accurate modeling of mineral solutions is important for tracing the condensation of the abundant rock-forming elements. For example, the melilite solid solution spans the composition range Ca₂Al₂SiO₇ – Ca₂MgSi₂O₇, and the stability of the Si-bearing end-member strongly influences the initial condensation of Si at high temperatures. Olivine spans the composition range Mg₂SiO₄ – Fe₂SiO₄ – MgCaSiO₄ and strongly affects the condensation of Fe as oxide at lower temperatures. Metal alloy incorporates fractions of Ni, Cr, and Co which vary with temperature. None of these mineral solutions exhibits ideal behavior.

The calculations follow chemical equilibrium with decreasing temperature, usually in 10º steps, at fixed pressure and bulk composition of the system. The effect of varying P^tot is explored for solar composition, and thereafter results are calculated at an arbitrarily chosen P^tot = 10³ dyn/cm², because the other cases exhibit variations with P^tot analogous to condensation of a vapor of solar composition. The assumption of even partial equilibrium between phases becomes less tenable as P^tot and T of the system decrease, so calculations are generally not pursued below P^tot = 10^-2 dyn/cm² and T = 1100 K. Because of the algorithms used in the minimization, calculations terminate at temperatures where the vapor phase becomes highly depleted (>10^-8) in one or more ultrarefractory elements. Major phases condensing below 1000 K are not addressed here, including iron sulfide (FeS), hydrated silicates (e.g., talc), water ice, ammonium and methane clathrates, and cryogenic gases [cf. Lewis, 1972].

In Figure 2 the distribution of atoms among various phases is illustrated as a function of temperature for condensation of a gas of solar composition at P^tot = 10³ dyn/cm². Corundum (Al₂O₃) is the first phase to condense, at ~1770 K, reacting with the gas to form hibonite (CaAl₁₂O₁₉) at ~1720 K, followed by a suite of Ca-aluminates and perovskite (CaTiO₃). Melilite, condensing at ~1590 K, is the first condensate modeled as a solid solution, and it incorporates increasing amounts of Mg and Si with decreasing temperature. At ~1460 K, metal alloy condenses, with ~19 mol % Ni, decreasing to 5.5% Ni by 1360 K. Metal is followed closely by Ca-pyroxene having the stoichiometry (Ca_1.0Mg_0.54Ti_0.43Al_0.92Si_1.12O₆) and nearly pure Mg-olivine (Mg₂SiO₄). Until nearly pure orthopyroxene (Mg₂Si₂O₆) condenses at ~1350 K, olivine contains most of the condensed Mg and Si. At solar bulk compositions, nearly all Fe condenses as metal, with almost no Fe entering silicates (as FeO) above ~600 K [Grossman, 1972]. The assemblage at 1200 K remains stable to well below 900 K. If feldspar (CaAl₂Si₂O₈) were to condense instead of cordierite (Mg₂Al₄Si₅O₁₈), substantial Na (and K) would begin to enter the feldspar lattice below 1000 K [Yoneda and Grossman, 1995, Figure 10].

Differences between earlier results, and the solar condensation sequence computed with the present code, have been reviewed by Ebel and Grossman (submitted manuscript, 1998). Ca-, Al-, Ti-rich oxide phases dominate at high T, but more than 80% of the matter condensable above 1000 K leaves the vapor phase with the condensation of olivine and metal, between 1450 and 1350 K. Because this is an equilibrium calculation, all the olivine (Mg/Si=2) is available to form orthopyroxene (Mg/Si=1) with the continued condensation of Si below 1350 K. In real stellar outflows some disequilibrium process, such as mantling, is more likely to obtain. The exact stability fields of the various calcium aluminates and cordierite depend strongly on the combination of thermodynamic data chosen to characterize each of them, and the available data are somewhat scattered (Ebel and Grossman, submitted manuscript, 1998). The overall systematics of Ca and Al condensation as oxides are, however, relatively insensitive to the identities of the mineral species at these high temperatures.

Another way to view the solar condensation sequence is to consider the calculated depletions of elements from the gas as a function of decreasing temperature, compared with observed depletions of the major rock-forming elements. Figure 3 illustrates selected ratios of elements that one would expect to observe in the gas phase at high temperatures during condensation from solar gas. In Figure 4, element depletions toward z Oph relative to solar are plotted at the temperatures where they match calculated depletions in the solar condensation sequence, shown as curves. Depletions relative to B star abundances (Z/Z_o~0.65) [Snow and Witt, 1996] are shown for comparison. It is apparent that there exists no single temperature at which a partially condensed cloud of solar composition could be "flash frozen" and enter the ISM with depletions matching those observed for these elements. At the conditions (1240 K and P^tot=10³ dyn/cm²) where Fe is calculated to condense as metal to a level matching its observed depletion, the refractory elements (Si and Mg) are 1 and 2 orders of magnitude more depleted than is observed, and the ultra-refractory elements (Ca, Al, and Ti) are even more so.

There is, however, a logical appeal to this link between condensation and depletion, as noted by Field [1974]. Consider the elements as three suites, (Ca, Al, and Ti), (Si and Mg), and (Fe, Ni, Co, and Cr), corresponding to the Ca-aluminates, olivine, and metal of the condensation sequence. For the elements considered in the condensation calculation, observed depletions decrease in the following order: Ti and Ca; Ni, Fe, Co, Cr, and Mn; Si, and Mg; and K, Na, P, and F. Note that Al cannot be reliably measured in dense clouds, owing to strong saturation of its commonly observed absorption line at 1670 Å, but its depletion may lie between those of Fe and Ti (D.E. Welty, personal communication, 1999). For each of the three suites of elements circled in Figure 1 there is a corresponding phase, or a group of closely related phases in the case of Ca-Ti-Al, in the solar condensation sequence. If the observed depletions of these elements in cold, dense (molecular) clouds are caused by their sequestration in grains, the formation of those grains by condensation at high temperature is strongly suggested by the results of the calculation. A circumstellar environment is the most likely place for such condensation to occur, although it may be that supernova shocks could create transient, localized environments conducive to high-temperature condensation in the ISM, an idea yet to be explored. The cooling time in such a process would be too short for equilibrium calculations to apply, however, and it is more likely that all available elements would condense, in their vapor phase abundances, as amorphous films on surviving grain cores behind the shock front. Repeated shocks would then impart a cosmic overprint to the stellar outflow condensation signature. In the cold, quiescent ISM it is unlikely that a grain formation mechanism exists which would sequester just these refractory elements in grains and in these groups so closely matching the major minerals. Depletion observations for some of t he less abundant, heavy elements support this view [Hobbs et al., 1993].

The effect of total pressure on the appearance temperatures of a few important condensate phases in a cooling gas of solar composition is shown in Figure 5. With decreasing total pressure the condensation temperatures of all the major solids decrease systematically, but the stability of metal is more sensitive to P^tot than the stabilities of the oxide phases are. For comparison with Figure 4, depletions of Ca, Si, and Fe observed toward z Oph match those calculated at ~1265, 1150, and 1060 K, respectively, at P^tot=1.0 dyn/cm², and at ~1582, 1440, and 1425 K, respectively, at P^tot=10⁵ dyn/cm². It is considered unlikely that stellar outflows reach the densities where P^tot ³ 10⁴ dyn/cm², at which silicate liquid consisting primarily of CaO+MgO+SiO₂+Al₂O₃ becomes stable, relative to solids (Ebel and Grossman, submitted manuscript, 1998). Such a liquid would presumably form as a mist of very fine, partially molten droplets, with agglomeration properties very different from those of solid condensates. Liquid droplets would likely quench to glass beads.

The condensates of C- and O-rich systems differ because the Cº O gas molecule is highly stable, so only the excess C or O is available to become the anion of condensates (e.g., SiC vs. SiO₂). The minerals TiC, SiC, and C (graphite) are likely to condense in the outflows of C-rich stars, and indeed these species occur as extrasolar grains in primitive meteorites [Bernatowicz at al., 1991]. Mineral stabilities at C/O > 1.0 have been explored in some detail by Larimer and Bartholomay [1979], Lodders and Fegley [1995], and Sharp and Wasserburg [1995], and the present calculation yields the same major features as theirs. The condensation temperatures of some of the major phases in systems with 0.8£ (C/O)£ 1.15 are shown in Figure 6. Solid-vapor phase relations are quite complex near C/O = 1.0. As C/O increases toward unity, oxide phases such as olivine draw oxygen from the vapor in sufficient quantity to create conditions reducing enough to stabilize small amounts of phases such as CaS, Fe₃C, SiC, and graphite. For the same reason, sequestration of C as TiC, SiC, and graphite at C/O > 1.01 liberates enough O so that small amounts of Al₂O₃ and Mg₂SiO₄ form. The algorithms used in the present calculations break down at ~1340 K for C/O>1.05, owing to extreme depletion of Ti from the gas phase, so the calculation was continued after the removal of all Ti and equivalent C from the system, a plausible simulation of fractional condensation. Calculations for C/O > 0.93 are sensitive to the solubility of Si in metal alloy. Here an ideal solid solution model for metal has been used above C/O=0.93, because calculated Si concentrations in metal alloy exceed 2 mol%, well above the range of activity data used to constrain the model of Ebel and Grossman (submitted manuscript, 1998).

Figures 7a and 7b illustrate the effect on depletion of increasing C/O in an otherwise solar gas, all at P^tot=10³ dyn/cm². For C/O<0.80 the calculated depletion curves resemble those for a gas of solar composition (C/O~0.42), but the phases present differ slightly. The temperatures at which feldspar, orthopyroxene, and cordierite condense drop steeply above C/O~0.83, as seen for orthopyroxene in Figure 6. At C/O=0.90, Fe, Mg, and Si condense to the z Oph depletion level at ~1265 K, ~1215 K, and below 1110 K, respectively. Si and Mg become increasingly decoupled at high C/O ratio, because Mg condenses as MgS and Si condenses as SiC. As C/O approaches 1.0, metal condenses at a slightly higher temperature relative to the oxide phases, and Si and Mg are much less depleted with decreasing temperature. Above C/O=1.0, Ti is extremely depleted relative to all other elements considered here, owing to the formation of TiC. For example, at C/O=1.1, P^tot=10³ dyn/cm², Ti is calculated to deplete to the z Oph level at ~1640 K. Si condenses as SiC until olivine appears, at progressively lower temperatures with increasing C/O. The effect of increasing C/O above ~0.90, for example, in the ejecta of massive C-rich stars, is to separate the Ca-Al-Ti and the Si-Mg groups noted above in the solar condensation sequence, so these elements reach their observed depletions over a much greater range of temperature than they do in any of the other cases investigated here.

In this scenario the abundances of all the elements except H and He are reduced to below solar abundances by a factor Z/Z_o, following Mathis [1996]. The effect of decreasing metallicity in this way to an extreme of Z/Z_o = 0.10 is very similar to that resulting from a slight increase in P^tot for a gas of the canonical solar composition. At Z/Z_o=0.10, P^tot=10³ dyn/cm², Ca, Si, and Fe become depleted to the z Oph levels at ~1320, 1200, and 1185 K, respectively, and depletion curves follow paths very similar to those for a gas of solar composition (Figure 4). The effect is to draw the depletion temperatures of the metal and olivine groups a bit closer together, but the Ca-Al-Ti group remains quite distinct.

Ebel and Grossman (submitted manuscript, 1998) have investigated the effect of enriching solar gas by up to 1000x in a dust of carbonaceous chondrite composition, taken as the meteorite Orgueil [Anders and Grevesse, 1989]. They found that at dust enrichments of ³ 13x, silicate liquid becomes stable, at P^tot = 10³ dyn/cm², but the enrichment required for liquid stability increases to >450x at P^tot = 1.0 dyn/cm². A dust of carbonaceous chondrite (C1) composition has a C/O ratio of 0.099, causing the dust-enriched system to be highly oxidizing. The effect of enriching the gas by a factor of 10 in this component is to dramatically increase the condensation temperatures of the refractory minerals. At P^tot=10³ dyn/cm², Ca, Si, and Fe become depleted to the z Oph levels at ~1510, 1340, and 1255 K, respectively. Because the ISM is depleted nearly equally in C and O, an interstellar dust (ISD) composition derived from the depletion data has C/O = 0.452. The depletion pattern for enrichment 10x in ISM dust is, however, nearly indistinguishable from that for 10xC1 dust.

Condensation sequences for several variations on the reference solar bulk compositions illustrate that plausible variations about this canonical bulk composition do not significantly alter the depletion patterns of the major refractory rock-forming elements. The depletion profiles for these various cases are quite similar in the temperature separation of the three groups of elements, Ca-Al-Ti, Fe-metal, and Si-Mg olivine. The solar reference composition therefore appears to remain a robust basis for discussion of the oxide grains which are likely to enter the ISM from stellar environments with C/O less than ~0.85. Yet these three element groups exhibit depletions inconsistent with isolation of a condensate + gas "package" at one particular temperature. Some systematic modification of chemical equilibrium during condensation or some differential destruction process in the ISM must be invoked to explain this.

One fact reiterated in these calculations is that Fe condenses as metal, not as FeO in silicates, from both C-rich and O-rich stellar environments. This metal contains, within reasonable uncertainty in the solid solution model utilized, all the Cr, Co, and Ni, which have depletions closely correlated to that of Fe. The existence of metal alloy as a significant component of interstellar dust has implications for models explaining the polarization of that dust and for the interaction of local interstellar dust with magnetic fields at the boundary of the heliosphere. Although the presence of oxidized Fe as a component of silicates is highly unlikely, it is possible that some significant fraction of the condensed metal grains becomes oxidized in the ISM [Duley, 1980], although recent work has confirmed that Fe-Ni metal alloy condenses with SiC from C-rich AGB stars and survives in meteorites [Bernatowicz et al., 1999]. Much of the difficulty of models requiring (Fe+Mg)³ (2*Si) disappears, if much or all of the Fe is present as metal or as isolated oxide grains rather than in silicates [Fitzpatrick, 1997].

Silicates are widely thought to comprise the nuclei, or cores, of some portion of the ISM dust. Here an identification of the composition and a partial identification of the crystal identity of a large fraction of the refractory grains formed in and around stars with C/O<1 have been made. Olivine (Mg₂SiO₄), metal (~90 atom % Fe), and some combination of Ca-titanates and aluminates emerge as by far the most probable grains making up the refractory cores of interstellar dust. Observations of the interstellar gas in the Small Magellanic Cloud (metallicities 0.2-0.25 solar) and of quasi-stellar object (QSO) absorption line systems (metallicities 0.05-0.5 solar) reveal gas phase abundances similar to those in low-density environments in our galaxy, suggesting that dust in all these regions could have similar composition [Lauroesch et al., 1996; Welty et al., 1997]. It could be that stardust, relatively consistent in composition despite a variety of sources, makes up, in fact, the bulk of the interstellar dust inferred to be responsible for the observed depletions in Ca, Al, Ti, Fe, Ni, Cr, Co, Si, and Mg. Any other explanation for the inferred dust compositions must depend on either (1) ad hoc, wildly nonsolar bulk compositions in stellar environments, forming, for example, fayalitic olivine (Fe_0.3Mg_1.7)SiO₄ in copious amounts, (2) disequilibrium processes very difficult to parameterize accurately or test experimentally, or (3) unspecified processes in the ISM which assemble, from cold, tenuous vapor, dust having a composition giving rise to the observed depletions.

A probe to analyze local interstellar dust, perhaps using mass spectrometry, could test these conclusions. As noted by Frisch et al. [1999], the STARDUST mission, expected to yield laboratory analyses of the most primitive solar nebula material yet, might return minimally processed presolar silicate dust. Dust with a (C/O<0.9) stellar heritage should consist of (Fe and Ni) metal, perhaps oxidized, and crystalline or amorphous (Ca,Al, and Ti) oxides and Mg silicate. If such grains dominate the ISM, as suggested here, distinct correlations should be observed among these elements, particularly in the composition of the smallest grain fraction. In contrast, dust grains produced following supernova destruction events should have entirely different compositions, reflecting cosmic abundances of the metals. An instrument capable of distinguishing between these two types of dust will be an essential component of the payload on the first interstellar probe mission.

Acknowledgments. The author thanks NASA for research support (NAGW-3340) and for travel funds through a grant (NAG 5-6625) to P. Frisch, the personnel and supporters of the International Space Science Institute for the forum, and D. E. Welty for a critical reading.
Janet G. Luhmann thanks Joseph Andrew Nuth III and another referee for their assistance in evaluating this paper.

References
Anders, E., and N. Grevesse, Abundances of the elements: Meteoritic and solar, Geochim. Cosmochim. Acta, 53, 197-214, 1989.
Bernatowicz, T. J., S. Amari, E.K. Zinner, and R.S. Lewis, Interstellar grains within interstellar grains, Astrophys. J. Lett., 373, 73-76, 1991.
Bernatowicz, T., J. Bradley, S. Amari, S. Messenger, and R. Lewis, New kinds of massive star condensates in a presolar graphite from Murchison, Lunar Planet. Sci. [CD-ROM], XXX, Abstract 1392, 1999.
Cardelli, J.A., The abundance of heavy elements in interstellar gas, Science, 265, 209-213, 1994.
Cardelli, J.A., D.M. Meyer, M. Jura, and B.D. Savage, The abundance of interstellar carbon, Astrophys. J., 467, 334-340, 1996.
Chase, M.W., Jr., C.A. Davies, J.R. Downey, D.J. Frurip, R.A. McDonald, and A.N. Syverud, JANAF thermochemical tables, 3rd ed., J. Phys. Chem. Ref. Data, 14, suppl. 1, 1856 pp., 1985.
Duley, W.W., Redox reactions and the optical properties of interstellar grains, Astrophys. J., 240, 950-955, 1980.
Ebel, D.S., and L. Grossman, Effect of dust enrichment on solid and liquid compositions in equilibrium with cosmic gases, Lunar Planet. Sci. [CD-ROM], XXIX, Abstract 1421, 1998.
Field, G.B., Interstellar abundances: Gas and dust, Astrophys. J., 187, 453-459, 1974.
Fitzpatrick, E.L., The abundance of Mg in the interstellar medium, Astrophys. J. Lett., 482, 199-202, 1997.
Frisch, P.C., et al., Dust in the local interstellar wind, Astrophys. J., in press, 1999.
Ghiorso, M.S., and R.O. Sack, Chemical mass transfer in magmatic processes, IV, A revised and internally consistent thermodynamic model for the interpolation and extrapolation of liquid-solid equilibria in magmatic systems at elevated temperatures and pressures, Contrib. Mineral. Petrol., 119, 197-212, 1995.
Grossman, L., Condensation in the primitive solar nebula, Geochim. Cosmochim. Acta, 36, 597-619, 1972.
Hobbs, L.M., D.E. Welty, D.C. Morton, L. Spitzer, and D.G. York, The interstellar abundances of tin and four other heavy elements, Astrophys. J., 411, 750-755, 1993.
Jenkins, E.B., Element abundances in the interstellar atomic material, in Interstellar Processes, edited by D.J. Hollenbach and H.A. Thronson Jr., pp. 533-560, D. Reidel, Norwell, Mass., 1987.
Larimer, J.W., and E. Anders, Chemical fractionation in meteorites, I, Condensation of the elements, Geochim. Cosmochim. Acta, 31, 1215-1238, 1967.
Larimer, J.W., and H.A. Bartholomay, The role of carbon and oxygen in cosmic gases: Some applications to the chemistry and mineralogy of enstatite chondrites, Geochim. Cosmochim. Acta, 43, 1455-1466, 1979.
Lattimer, J.M., D. N. Schramm, and L. Grossman, Condensation in supernova ejecta and isotopic anomalies in meteorites, Astrophys. J., 219, 230-249, 1978.
Lauroesch, J.T., J.W. Truran, D.E. Welty, and D.G. York, QSO absorption-line systems and early chemical evolution, Publ. Astron. Soc. Pac., 108, 641-658, 1996.
Lewis, J.S., Low temperature condensation from the solar nebula, Icarus, 16, 241-252, 1972.
Lodders, K., and B. Fegley Jr., The origin of circumstellar silicon carbide grains found in meteorites, Meteoritics Planet. Sci., 30, 661-678, 1995.
Mathis, J.S., Dust models with tight abundance constraints, Astrophys. J., 472, 643-655, 1996.
Meyer, D.M., Interstellar depletions and the composition of interstellar dust grains, in Astrophysical Implications of the Laboratory Study of Presolar Materials, edited by T.J. Bernatowicz and E. Zinner, AIP Conf. Proc., 402, 507-522, 1997.
Nittler, L.R., Presolar oxide grains in meteorites, in Astrophysical Implications of the Laboratory Study of Presolar Materials, edited by T.J. Bernatowicz and E. Zinner, AIP Conf. Proc., 402, 59-84, 1997.
Seab, C.G., Grain destruction, formation, and evolution, in Interstellar Processes, edited by D.J. Hollenbach and H.A. Thronson Jr., pp. 491-512, D. Reidel, Norwell, Mass., 1987.
Sharp, C.M., and G.J. Wasserburg, Molecular equilibria and condensation temperatures in carbon-rich gases, Geochim. Cosmochim. Acta, 59, 1633-1652, 1995.
Shu, F., J. Najita, E. Ostriker, F. Wilken, S. Ruden, and S. Lizano, Magnetocentrifugally driven flows from young stars and disks, I, A generalized model, Astrophys. J., 429, 781-796, 1994.
Snow, T., The depletion of interstellar elements and the interaction between gas and dust in space, Astrophys. J. Lett., 202, 87-90, 1975.
Snow, T.P., and A.N. Witt, Interstellar depletions updated: Where all the atoms went, Astrophys. J. Lett., 468, 65-68, 1996.
Tielens, A.G.G.M., Interstellar depletions and the life cycle of interstellar dust, Astrophys. J., 499, 267-272, 1998.
Wasson, J.T., Meteorites: Their Record of Early Solar System History, 267 pp., W.H. Freeman, New York, 1985.
Welty, D.E., J.T. Lauroesch, J.C. Blades, L.M. Hobbs, and D.G. York, Interstellar abundances in the Magellanic clouds, I, GHRS observations of the Small Magellanic Cloud star Sk 108, Astrophys. J., 489, 672-692, 1997.
Wooden, D. H., Observational evidence for mixing and dust condensation in core-collapse supernovae, in Astrophysical Implications of the Laboratory Study of Presolar Materials, edited by T.J. Bernatowicz and E. Zinner, AIP Conf. Proc., 402, 317-378, 1997.
Yoneda, S., and L. Grossman, Condensation of CaO-MgO-Al₂O₃-SiO₂ liquids from cosmic gases, Geochim. Cosmochim. Acta, 59, 3413-3444, 1995.
________________
D.S. Ebel, Department of Geophysical Sciences, The University of Chicago, 5734 South Ellis Ave., Chicago, IL 60637.
(Received February 16, 1999; revised April 20, 1999; accepted April 23, 1999)
ÓCopyright 1999 by the American Geophysical Union, Paper number 1999JA900192
0148-0227/99/1999JA900192$09.00

Figure 1. Observed depletions for the main, cold, dense molecular component toward z Oph [Jenkins, 1987; Cardelli, 1994; Hobbs et al., 1993; after Field, 1974] (modified by D.E. Welty, personal communication, 1997), where depletion_i = log[(A_i^observed/A_i^observed)*(A_H^solar/A_H^ISM)] and the "condensation temperature" for each element is from Wasson [1985, Table G-1].

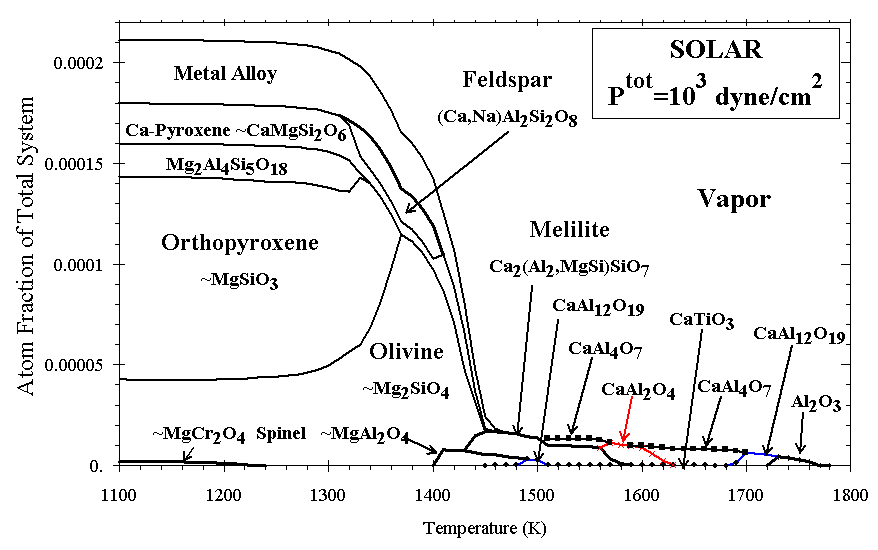
Figure 2. Condensation of atoms to minerals from solar gas.

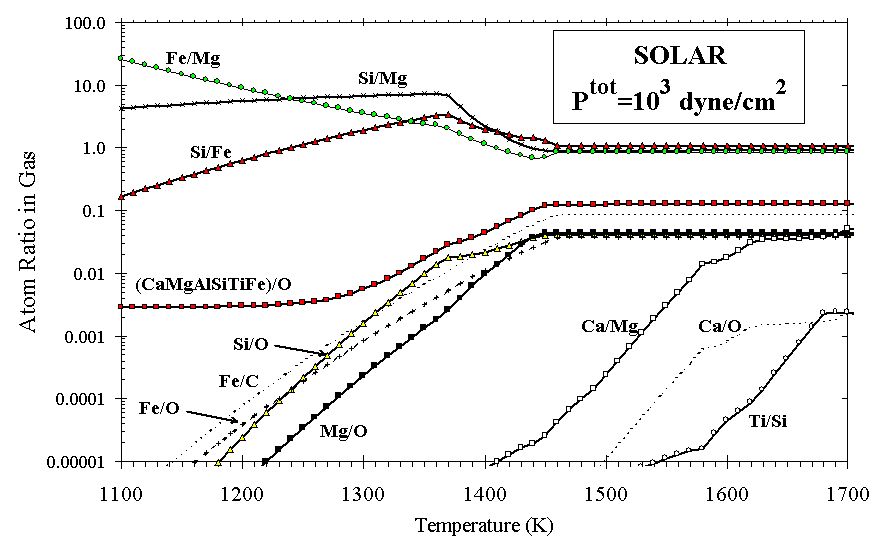
Figure 3. The ratios of atoms remaining in the gas fraction during condensation from a gas of solar composition.

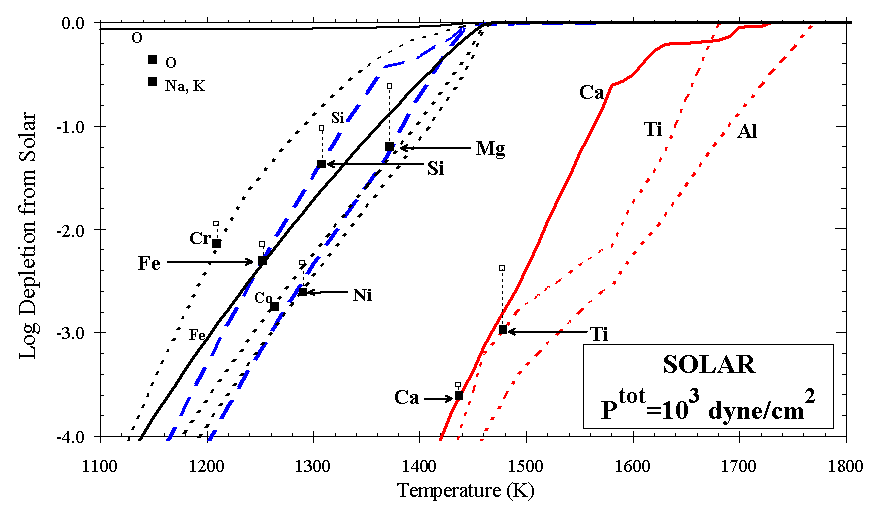
Figure 4. Depletion of atoms from the gas phase for condensation from solar bulk composition. Observed depletions toward z Oph relative to solar (D.E. Welty, personal communication, 1999) are plotted as solid squares at the temperatures where they match those calculated, except for O, Na, and K. Corresponding depletions from B star abundances [Snow and Witt, 1996] are plotted as open squares.

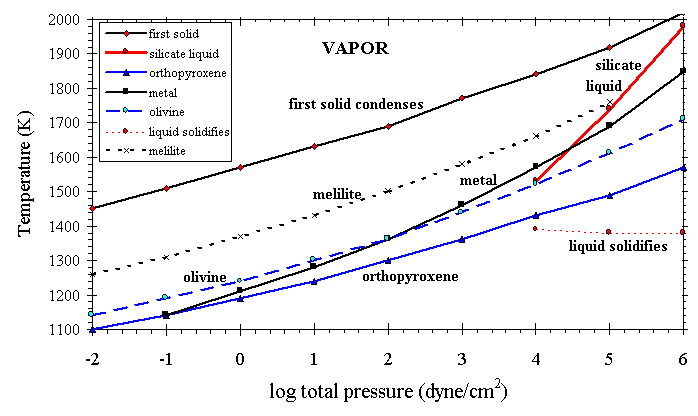
Figure 5. Effect of pressure on first condensation of selected phases from a vapor of solar composition.

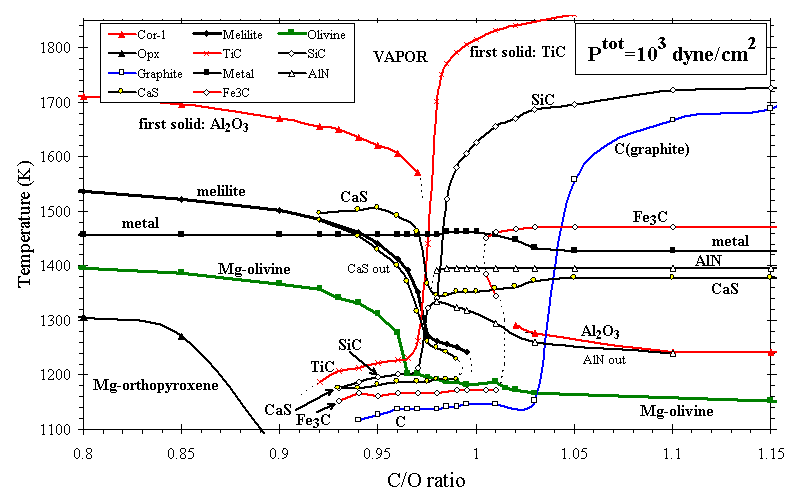
Figure 6. Condensation temperatures of selected major phases in C-enriched systems with 0.8£ (C/O)£ 1.15 at P^tot=10³ dyn/cm². Symbols are calculated values.

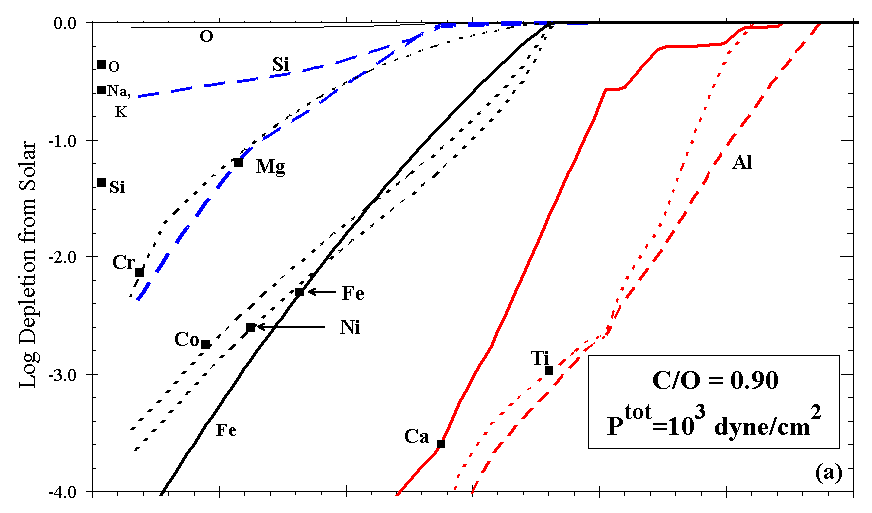
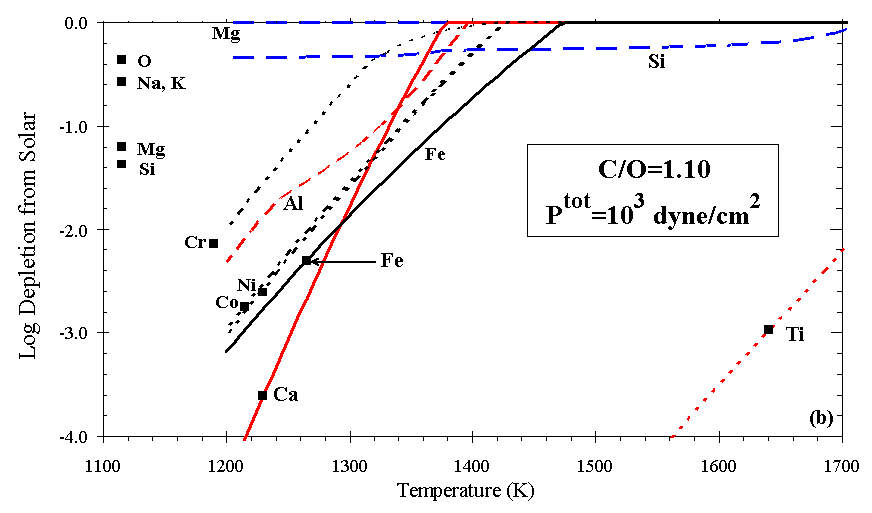
Figure 7. Depletions as C is added to solar gas for (a) C/O=0.90 and (b) C/O=1.10.